Hands-on Exercise 5b: Local Measures of Spatial Autocorrelation

1 Overview

Local Measures of Spatial Autocorrelation (LMSA) focuses on the relationships between each observation and its surroundings, rather than providing a single summary of these relationships across the map. In this sense, they are not summary statistics but scores that allow us to learn more about the spatial structure in our data.

The general intuition behind the metrics however is similar to that of global ones. Some of them are even mathematically connected, where the global version can be decomposed into a collection of local ones.

An example is Local Indicators of Spatial Association (LISA). Beside LISA, Getis-Ord’s Gi-statistics will be introduce as an alternative LISA statistics that present complementary information or allow us to obtain similar insights for geographically referenced data.

This is an extension of Hands-on Exercise 5a, parts 1 to 4.2 follows the previous exercise.

The Analytical Question

In spatial policy, one of the main development objective of the local government and planners is to ensure equal distribution of development in the province. Our task in this study, hence, is to apply appropriate spatial statistical methods to discover if development are even distributed geographically. If the answer is No, then, our next question will be “is there sign of spatial clustering?” And, if the answer for this question is Yes, then our next question will be “where are these clusters?”

In this case study, we are interested to examine the spatial pattern of a selected development indicator (i.e. GDP per capita) of Hunan Provice, People Republic of China.

2 The Packages

Packages

Package	Description
spdep	To compute spatial weights, Global and Local Spatial Autocorrelation statistics (eg plot Moran scatterplot, compute and plot correlogram)
sf	For importing, managing, and processing geospatial data
tidyverse	A collection of functions for performing data science task such as importing, tidying, wrangling data and visualising data.
tmap	To prepare cartographic quality choropleth map
DT, knitr and kableExtra	For building tables

Code

pacman::p_load(sf, spdep, 
               tmap, 
               tidyverse, 
               DT, knitr, kableExtra)

# -   Creates a package list containing the necessary R packages
# -   Checks if the R packages in the package list have been installed
# -   If not installed, will installed the missing packages & launch into R environment.

3 The Data

Two data sets will be used in this hands-on exercise, they are:

Type	Name	Details
Geospatial	Hunan	County boundary layer Format: SHP (ESRI Shapefile)
Aspatial	Hunan_2012	Contains selected Hunan’s local development indicators in 2012 Format: CSV

3.1 Loading the Data

In this section, you will learn how to bring a geospatial data and its associated attribute table into R environment. The geospatial data is in ESRI shapefile format and the attribute table is in csv fomat.

Import shapefile

The code chunk below uses st_read() of sf package to import Hunan shapefile into R.

#output: simple features object

hunan <- st_read(dsn = "data/geospatial", 
                 layer = "Hunan")

Reading layer `Hunan' from data source 
  `C:\kytjy\ISSS626-GAA\Hands-on_Ex\Hands-on_Ex05\data\geospatial' 
  using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84

NAME_2	ID_3	NAME_3	ENGTYPE_3	Shape_Leng	Shape_Area	County	geometry
Changde	21098	Anxiang	County	1.8690742	0.1005619	Anxiang	POLYGON ((112.0625 29.75523...
Changde	21100	Hanshou	County	2.3606914	0.1997875	Hanshou	POLYGON ((112.2288 29.11684...
Changde	21101	Jinshi	County City	1.4256199	0.0530241	Jinshi	POLYGON ((111.8927 29.6013,...
Changde	21102	Li	County	3.4743245	0.1890812	Li	POLYGON ((111.3731 29.94649...
Changde	21103	Linli	County	2.2895061	0.1145036	Linli	POLYGON ((111.6324 29.76288...
Changde	21104	Shimen	County	4.1719181	0.3719471	Shimen	POLYGON ((110.8825 30.11675...
Changsha	21109	Liuyang	County City	4.0605788	0.4601679	Liuyang	POLYGON ((113.9905 28.5682,...
Changsha	21110	Ningxiang	County	3.3237542	0.2661420	Ningxiang	POLYGON ((112.7181 28.38299...
Changsha	21111	Wangcheng	County	2.2920930	0.1304916	Wangcheng	POLYGON ((112.7914 28.52688...
Chenzhou	21112	Anren	County	2.2407387	0.1334394	Anren	POLYGON ((113.1757 26.82734...
Chenzhou	21115	Guidong	County	2.0467289	0.1285299	Guidong	POLYGON ((114.1799 26.20117...
Chenzhou	21117	Jiahe	County	1.5038242	0.0631237	Jiahe	POLYGON ((112.4425 25.74358...
Chenzhou	21118	Linwu	County	2.0512481	0.1244964	Linwu	POLYGON ((112.5914 25.55143...
Chenzhou	21119	Rucheng	County	2.7155640	0.2176296	Rucheng	POLYGON ((113.6759 25.87578...
Chenzhou	21120	Yizhang	County	3.2765386	0.1935418	Yizhang	POLYGON ((113.2621 25.68394...
Chenzhou	21121	Yongxing	County	2.9211528	0.1767181	Yongxing	POLYGON ((113.3169 26.41843...
Chenzhou	21122	Zixing	County City	2.6995368	0.2476280	Zixing	POLYGON ((113.7311 26.16259...
Hengyang	21123	Changning	County City	2.4013569	0.1863642	Changning	POLYGON ((112.6144 26.60198...
Hengyang	21124	Hengdong	County	2.7098301	0.1756985	Hengdong	POLYGON ((113.1056 27.21007...
Hengyang	21125	Hengnan	County	3.7804926	0.2408050	Hengnan	POLYGON ((112.7599 26.98149...
Hengyang	21126	Hengshan	County	2.3513543	0.0899128	Hengshan	POLYGON ((112.607 27.4689, ...
Hengyang	21129	Leiyang	County	2.7427498	0.2426073	Leiyang	POLYGON ((112.9996 26.69276...
Hengyang	21130	Qidong	County	3.0714217	0.1733332	Qidong	POLYGON ((111.7818 27.0383,...
Huaihua	21131	Chenxi	County	3.0228314	0.1821929	Chenxi	POLYGON ((110.2624 28.21778...
Huaihua	21134	Zhongfang	County	2.9023763	0.1994978	Zhongfang	POLYGON ((109.9431 27.72858...
Huaihua	21135	Huitong	County	3.1096821	0.2053454	Huitong	POLYGON ((109.9419 27.10512...
Huaihua	21136	Jingzhou	County	2.8584583	0.1988991	Jingzhou	POLYGON ((109.8186 26.75842...
Huaihua	21137	Mayang	Autonomous County	2.3274351	0.1462606	Mayang	POLYGON ((109.795 27.98008,...
Huaihua	21138	Tongdao	Autonomous County	2.5711292	0.2021613	Tongdao	POLYGON ((109.9294 26.46561...
Huaihua	21139	Xinhuang	Autonomous County	2.1443973	0.1377764	Xinhuang	POLYGON ((109.227 27.43733,...
Huaihua	21140	Xupu	County	4.0350213	0.3136471	Xupu	POLYGON ((110.7189 28.30485...
Huaihua	21141	Yuanling	County	4.1642914	0.5345233	Yuanling	POLYGON ((110.9652 28.99895...
Huaihua	21142	Zhijiang	Autonomous County	2.4452310	0.1906027	Zhijiang	POLYGON ((109.8818 27.60661...
Loudi	21143	Lengshuijiang	County City	0.9753557	0.0372343	Lengshuijiang	POLYGON ((111.5307 27.81472...
Loudi	21146	Shuangfeng	County	2.4012680	0.1565776	Shuangfeng	POLYGON ((112.263 27.70421,...
Loudi	21147	Xinhua	County	3.3284533	0.3361624	Xinhua	POLYGON ((111.3345 28.19642...
Shaoyang	21148	Chengbu	Autonomous County	2.9374722	0.2362023	Chengbu	POLYGON ((110.4455 26.69317...
Yongzhou	21149	Dongan	District	3.2132100	0.1983914	Dongan	POLYGON ((111.4531 26.86812...
Shaoyang	21150	Dongkou	County	2.9425568	0.1971258	Dongkou	POLYGON ((110.6622 27.37305...
Shaoyang	21151	Longhui	County	2.7208650	0.2578820	Longhui	POLYGON ((110.985 27.65983,...
Shaoyang	21152	Shaodong	County	2.3029031	0.1701016	Shaodong	POLYGON ((111.9054 27.40254...
Shaoyang	21155	Suining	County	3.3043615	0.2659378	Suining	POLYGON ((110.389 27.10006,...
Shaoyang	21156	Wugang	County City	2.2565865	0.1400498	Wugang	POLYGON ((110.9878 27.03345...
Shaoyang	21157	Xinning	County	3.3414094	0.2487593	Xinning	POLYGON ((111.0736 26.84627...
Shaoyang	21158	Xinshao	County	2.2955891	0.1658312	Xinshao	POLYGON ((111.6013 27.58275...
Xiangtan	21159	Shaoshan	County City	0.7722034	0.0212792	Shaoshan	POLYGON ((112.5391 27.97742...
Xiangtan	21162	Xiangxiang	County City	3.0755761	0.1840808	Xiangxiang	POLYGON ((112.4549 28.05783...
Xiangxi Tujia and Miao	21163	Baojing	County	2.5569785	0.1606901	Baojing	POLYGON ((109.7015 28.82844...
Xiangxi Tujia and Miao	21164	Fenghuang	County	2.2928893	0.1596618	Fenghuang	POLYGON ((109.5239 28.19206...
Xiangxi Tujia and Miao	21165	Guzhang	County	1.7973808	0.1202073	Guzhang	POLYGON ((109.8968 28.74034...
Xiangxi Tujia and Miao	21166	Huayuan	County	1.7921938	0.1025162	Huayuan	POLYGON ((109.5647 28.61712...
Xiangxi Tujia and Miao	21167	Jishou	County City	1.8826069	0.0973363	Jishou	POLYGON ((109.8375 28.4696,...
Xiangxi Tujia and Miao	21168	Longshan	County	2.9782522	0.2919091	Longshan	POLYGON ((109.6337 29.62521...
Xiangxi Tujia and Miao	21169	Luxi	County	2.2051733	0.1434018	Luxi	POLYGON ((110.1067 28.41835...
Xiangxi Tujia and Miao	21170	Yongshun	County	3.0959707	0.3551324	Yongshun	POLYGON ((110.0003 29.29499...
Yiyang	21171	Anhua	County	4.5835050	0.4510648	Anhua	POLYGON ((111.6034 28.63716...
Yiyang	21172	Nan	County	2.3011103	0.1247939	Nan	POLYGON ((112.3232 29.46074...
Yiyang	21176	Yuanjiang	County City	2.3268236	0.1886048	Yuanjiang	POLYGON ((112.4391 29.1791,...
Yongzhou	21178	Jianghua	Autonomous County	3.3360379	0.2927690	Jianghua	POLYGON ((111.6461 25.29661...
Yongzhou	21180	Lanshan	County	2.3556792	0.1603531	Lanshan	POLYGON ((112.2286 25.61123...
Yongzhou	21183	Ningyuan	County	3.3322291	0.2266737	Ningyuan	POLYGON ((112.0715 26.09892...
Yongzhou	21185	Shuangpai	County	2.3877440	0.1540255	Shuangpai	POLYGON ((111.8864 26.11957...
Yongzhou	21186	Xintian	County	1.7274574	0.0894019	Xintian	POLYGON ((112.2578 26.0796,...
Yueyang	21187	Huarong	County	2.8178435	0.1678359	Huarong	POLYGON ((112.9242 29.69134...
Yueyang	21188	Linxiang	County City	2.5975997	0.1568525	Linxiang	POLYGON ((113.5502 29.67418...
Yueyang	21189	Miluo	County City	2.4474057	0.1497881	Miluo	POLYGON ((112.9902 29.02139...
Yueyang	21190	Pingjiang	County	3.2177944	0.3786800	Pingjiang	POLYGON ((113.8436 29.06152...
Yueyang	21191	Xiangyin	County	2.3515063	0.1491429	Xiangyin	POLYGON ((112.9173 28.98264...
Zhangjiajie	21194	Cili	County	2.8940385	0.3232206	Cili	POLYGON ((110.8822 29.69017...
Zhuzhou	21197	Chaling	County	2.2375615	0.2278921	Chaling	POLYGON ((113.7666 27.10573...
Zhuzhou	21198	Liling	County City	2.2435440	0.1960655	Liling	POLYGON ((113.5673 27.94346...
Zhuzhou	21199	Yanling	County	2.1078954	0.1849090	Yanling	POLYGON ((113.9292 26.6154,...
Zhuzhou	21200	You	County	2.8904505	0.2436366	You	POLYGON ((113.5879 27.41324...
Zhuzhou	21201	Zhuzhou	District	0.9331877	0.0373488	Zhuzhou	POLYGON ((113.2493 28.02411...
Zhangjiajie	21196	Sangzhi	County	3.3475449	0.3216362	Sangzhi	POLYGON ((110.556 29.40543,...
Yueyang	21192	Yueyang	District	2.5710437	0.1047594	Yueyang	POLYGON ((113.343 29.61064,...
Yongzhou	21184	Qiyang	County	3.1835301	0.2275458	Qiyang	POLYGON ((111.5563 26.81318...
Yiyang	21173	Taojiang	County	2.6080229	0.1905982	Taojiang	POLYGON ((112.0508 28.67265...
Shaoyang	21153	Shaoyang	County City	0.9765399	0.0316779	Shaoyang	POLYGON ((111.5013 27.30207...
Loudi	21144	Lianyuan	County City	2.8007253	0.2057341	Lianyuan	POLYGON ((111.6789 28.02946...
Huaihua	21132	Hongjiang	District	3.3031522	0.1994795	Hongjiang	POLYGON ((110.1441 27.47513...
Hengyang	21127	Hengyang	County City	0.9035944	0.0349171	Hengyang	POLYGON ((112.7144 26.98613...
Chenzhou	21116	Guiyang	County	3.6939698	0.2668106	Guiyang	POLYGON ((113.0811 26.04963...
Changsha	21107	Changsha	District	0.9536480	0.0320942	Changsha	POLYGON ((112.9421 28.03722...
Changde	21105	Taoyuan	County	4.1225866	0.4126555	Taoyuan	POLYGON ((112.0612 29.32855...
Xiangtan	21160	Xiangtan	County City	0.8480602	0.0253653	Xiangtan	POLYGON ((113.0426 27.8942,...
Yongzhou	21177	Dao	County	2.7674949	0.2206642	Dao	POLYGON ((111.498 25.81679,...
Yongzhou	21179	Jiangyong	County	2.2995970	0.1473782	Jiangyong	POLYGON ((111.3659 25.39472...

Import csv file

Next, we will import Hunan_2012.csv into R by using read_csv() of readr package.

#output: R dataframe class

hunan2012 <- read_csv("data/aspatial/Hunan_2012.csv")

County	City	avg_wage	deposite	FAI	Gov_Rev	Gov_Exp	GDP	GDPPC	GIO	Loan	NIPCR	Bed	Emp	EmpR	EmpRT	Pri_Stu	Sec_Stu	Household	Household_R	NOIP	Pop_R	RSCG	Pop_T	Agri	Service	Disp_Inc	RORP	ROREmp
Anhua	Yiyang	30544	10967.0	6831.7	456.72	2703.00	13225.0	14567	9276.90	3954.90	3528.3	2718	494.310	441.4	338.0	54.175	32.830	290.400	234.5	101	670.3	5760.60	910.8	4942.253	5414.5	12373	0.7359464	0.8929619
Anren	Chenzhou	28058	4598.9	6386.1	220.57	1454.70	4941.2	12761	4189.20	2555.30	3271.8	970	290.820	255.4	99.4	33.171	17.505	104.600	121.9	34	243.2	2386.40	388.7	2357.764	3814.1	16072	0.6256753	0.8782065
Anxiang	Changde	31935	5517.2	3541.0	243.64	1779.50	12482.0	23667	5108.90	2806.90	7693.7	1931	336.390	270.5	205.9	19.584	17.819	148.100	135.4	53	346.0	3957.90	528.3	4524.410	14100.0	16610	0.6549309	0.8041262
Baojing	Hunan West	30843	2250.0	1005.4	192.59	1379.10	4087.9	14563	3623.50	1253.70	4191.3	927	195.170	145.6	116.4	19.249	11.831	73.200	69.9	18	184.1	768.04	281.3	1118.561	541.8	13455	0.6544614	0.7460163
Chaling	Zhuzhou	31251	8241.4	6508.4	620.19	1947.00	11585.0	20078	9157.70	4287.40	3887.7	1449	330.290	299.0	154.0	33.906	20.548	148.700	139.4	106	301.6	4009.50	578.4	3793.550	5444.0	20461	0.5214385	0.9052651
Changning	Hengyang	28518	10860.0	7920.0	769.86	2631.60	19886.0	24418	37392.00	4242.80	9528.0	3605	548.610	415.1	273.7	81.831	44.485	211.200	211.7	115	448.2	5220.40	816.3	6430.782	13074.6	20868	0.5490628	0.7566395
Changsha	Changsha	54540	24332.0	33624.0	5350.00	7885.50	88009.0	88656	51361.00	40534.00	17070.0	3310	670.820	452.0	219.4	59.151	39.685	300.300	248.4	214	475.1	22604.00	998.6	13107.148	17726.6	183252	0.4757661	0.6738022
Chengbu	Shaoyang	28597	2580.6	1922.3	160.73	1191.60	2569.5	10132	1681.40	1232.00	3271.8	582	162.480	127.6	94.4	18.751	7.869	76.100	59.6	17	189.6	1173.80	256.7	1356.950	1215.1	12379	0.7386054	0.7853274
Chenxi	Huaihua	33580	4990.0	5818.4	460.49	1724.20	7755.2	17026	6644.50	3220.00	4777.0	2170	308.430	214.4	174.8	26.706	14.591	139.500	110.5	55	311.7	2570.60	456.7	2257.520	1306.3	14595	0.6825049	0.6951334
Cili	Zhangjiajie	33099	8116.9	4498.1	499.77	2306.20	11378.0	18714	5843.30	5503.40	5031.8	2179	381.200	334.8	264.3	34.918	27.020	211.400	174.5	70	379.4	3116.90	610.4	3112.731	5005.6	15603	0.6215596	0.8782791
Dao	Yongzhou	32541	7245.0	7922.0	461.66	2013.50	11034.0	18059	2393.80	2873.50	9000.0	1588	381.530	344.3	178.3	65.790	31.430	158.700	157.9	44	388.2	2898.80	613.6	5602.035	8411.1	16305	0.6326597	0.9024192
Dongan	Yongzhou	36713	6549.3	9158.0	434.07	1720.60	11495.0	20901	11597.00	3320.60	9116.7	1305	322.250	278.1	163.6	39.419	20.661	166.500	163.0	84	366.0	3106.30	551.2	4866.481	6784.4	20265	0.6640058	0.8629946
Dongkou	Shaoyang	31483	9489.6	8703.2	374.96	2209.50	10286.0	13240	10568.00	4120.30	3792.5	1620	583.560	499.2	263.2	69.845	43.194	262.400	220.4	74	523.1	3229.10	780.9	6025.184	9116.8	15375	0.6698681	0.8554390
Fenghuang	Hunan West	31608	4008.7	2550.0	406.51	1763.60	4681.2	13382	848.99	2863.00	4681.2	1212	250.730	195.4	151.8	33.379	17.690	90.100	80.5	17	255.5	2605.40	351.3	1206.261	651.1	14281	0.7272986	0.7793244
Guidong	Chenzhou	30149	2200.1	2512.9	111.19	880.00	1955.9	8497	1202.60	1437.20	3130.4	567	138.530	115.2	56.9	13.437	7.091	64.800	65.4	14	150.1	486.10	231.8	630.016	911.1	12290	0.6475410	0.8315888
Guiyang	Chenzhou	41394	9664.8	15712.0	1309.20	2727.50	23023.0	32853	36820.00	4860.10	10271.0	2237	517.180	430.9	242.0	69.344	33.568	231.800	217.5	127	420.4	6281.80	704.1	8804.639	14791.5	64517	0.5970743	0.8331722
Guzhang	Hunan West	28610	1563.8	1021.7	108.40	959.60	1490.4	11580	513.95	849.56	3595.9	392	98.421	74.6	56.7	8.718	6.288	35.200	31.4	10	85.2	354.48	129.0	527.230	504.0	11954	0.6604651	0.7579683
Hanshou	Changde	32265	7979.0	8665.0	386.13	2062.40	15788.0	20981	13491.00	4550.00	8269.9	2560	456.780	388.8	246.7	42.097	33.029	240.200	208.7	95	553.2	4460.50	804.6	6545.350	17727.0	18925	0.6875466	0.8511756
Hengdong	Hengyang	30992	8661.0	6665.0	542.25	1937.40	17409.0	27485	17305.00	4118.00	10829.0	1859	388.340	284.5	201.0	48.983	36.120	164.400	167.4	96	426.4	5127.00	634.9	5972.961	11278.5	19800	0.6716018	0.7326054
Hengnan	Hengyang	28031	3288.9	9531.4	804.91	2894.40	21019.0	21911	20953.00	4013.00	9872.9	2173	601.570	503.6	354.0	76.933	57.519	256.000	274.3	118	629.1	5752.60	961.4	8624.680	15914.0	18683	0.6543582	0.8371428
Hengshan	Hengyang	28688	5944.6	4871.1	451.46	1393.70	9718.9	25172	8571.50	2221.50	10619.0	966	291.120	261.9	158.8	28.997	20.909	103.700	101.0	89	256.4	1713.70	387.0	3505.269	6233.5	17732	0.6625323	0.8996290
Hengyang	Hengyang	27760	14680.0	11145.0	597.66	2778.80	21495.0	19382	18288.00	5549.60	10313.0	2632	686.520	500.2	313.6	88.917	64.674	299.200	247.7	120	733.4	5386.30	1111.6	12451.938	23139.2	124392	0.6597697	0.7286022
Hongjiang	Huaihua	37686	5966.0	6515.5	623.95	2067.80	7355.5	17733	13750.00	3272.20	6553.5	1161	229.400	199.9	132.0	23.614	18.837	136.100	124.7	76	260.9	1744.20	415.8	2588.250	202.8	27334	0.6274651	0.8714037
Huarong	Yueyang	26832	8116.4	14292.0	365.84	1933.90	21654.0	30413	40193.00	4564.80	10367.0	1500	442.970	359.2	252.9	31.601	26.933	202.300	170.2	151	430.3	6348.90	714.1	7690.520	10050.6	21501	0.6025767	0.8108901
Huayuan	Hunan West	31708	3669.8	2200.0	331.78	1503.70	5905.9	20337	9257.60	2463.60	4353.8	1240	214.790	149.8	94.9	23.831	14.031	76.900	59.9	74	188.1	1024.70	291.1	883.722	533.2	15467	0.6461697	0.6974254
Huitong	Huaihua	33693	4615.0	2617.4	295.00	1306.70	4588.3	14334	2095.60	1369.30	4631.9	1194	246.150	193.5	143.7	20.603	13.337	96.700	114.4	25	234.5	1061.70	320.9	1580.090	5.2	13989	0.7307572	0.7861060
Jiahe	Chenzhou	36023	5493.1	4864.3	453.68	1331.50	9608.2	32091	14882.00	1906.50	7903.3	719	242.800	198.9	83.0	36.054	19.497	99.000	108.5	100	179.6	1365.90	301.3	2276.272	3230.2	17744	0.5960836	0.8191928
Jianghua	Yongzhou	34378	4586.4	4631.5	309.70	1651.40	6555.9	15801	3357.10	2976.00	3225.3	1663	306.310	272.7	188.9	37.494	20.644	109.900	116.1	33	285.1	2384.80	416.7	3272.511	10533.8	16274	0.6841853	0.8902746
Jiangyong	Yongzhou	30250	3198.2	3942.5	187.23	1009.10	4012.2	17168	2022.70	1201.20	3253.9	720	153.580	132.8	94.3	21.936	11.093	68.300	61.2	25	163.5	1238.20	234.3	2862.901	9773.3	16634	0.6978233	0.8646959
Jingzhou	Huaihua	33870	3592.8	2031.4	237.51	1129.00	5007.7	20348	4534.10	1566.50	5397.3	1054	163.910	112.6	85.8	16.978	11.446	69.100	56.1	32	140.6	1611.50	246.7	1769.328	337.5	12859	0.5699230	0.6869624
Jinshi	Changde	28692	4581.7	4777.0	373.31	1148.40	8706.9	34592	10935.00	2242.00	8169.9	848	122.780	82.1	61.7	8.723	7.592	81.900	43.7	77	92.4	3683.00	251.8	2562.460	7525.0	19498	0.3669579	0.6686757
Jishou	Hunan West	39816	9586.2	5235.0	470.22	1738.20	9631.5	31537	6345.70	8282.90	4823.0	3790	213.420	97.0	62.4	25.454	21.941	99.200	46.5	49	85.2	5651.00	306.6	849.010	611.6	17980	0.2778865	0.4545029
Lanshan	Yongzhou	33756	4236.0	3986.7	296.68	1194.60	6627.2	20088	5392.10	1599.40	8672.1	1144	233.390	201.5	131.6	32.448	16.299	83.300	90.7	52	198.2	2234.20	330.9	2262.021	10341.9	19161	0.5989725	0.8633618
Leiyang	Hengyang	32814	15393.0	18687.0	1535.20	3819.00	30213.0	26105	42707.00	7409.20	10611.0	2531	750.120	553.7	405.8	112.200	56.350	338.100	281.2	155	629.3	7268.10	1160.2	8349.199	19981.6	19634	0.5424065	0.7381486
Lengshuijiang	Loudi	35647	6805.3	9746.8	1054.20	2105.30	21243.0	64257	36926.00	8936.60	10441.0	1413	191.320	101.8	61.8	29.639	20.113	112.400	56.9	118	78.4	5750.60	332.6	1277.869	991.8	23120	0.2357186	0.5320928
Li	Changde	32541	13487.0	16066.0	709.61	2459.50	20322.0	24473	18402.00	6748.00	8377.0	2038	513.440	426.8	227.1	38.975	33.938	268.500	256.0	96	539.7	7110.20	832.5	7562.340	53160.0	18985	0.6482883	0.8312558
Lianyuan	Loudi	30320	8059.7	9255.3	707.45	3298.60	18340.0	18346	20515.00	7243.20	4307.7	2260	706.840	612.9	344.1	71.232	53.597	316.200	298.7	154	712.6	6889.00	1001.5	7642.158	5965.4	38131	0.7115327	0.8670986
Liling	Zhuzhou	42896	12865.0	19125.0	2602.60	4221.40	39553.0	41491	57146.00	9398.10	13347.0	2797	639.830	513.1	212.1	53.992	33.705	248.400	229.7	482	473.2	11213.00	958.0	5373.990	17378.0	24185	0.4939457	0.8019318
Linli	Changde	32667	564.1	7781.2	336.86	1538.70	10355.0	25554	8214.00	358.00	8143.1	1440	307.360	272.2	100.8	23.286	18.943	129.100	157.2	99	246.6	3604.90	409.3	3583.910	7031.0	18604	0.6024921	0.8856065
Linwu	Chenzhou	32031	5984.0	5734.3	478.92	1435.20	8191.1	23986	6250.70	2152.70	7102.2	959	215.300	184.1	90.2	41.913	13.238	101.500	88.0	67	227.5	2023.30	342.8	1606.947	2632.2	17966	0.6636523	0.8550859
Linxiang	Yueyang	31669	5850.5	10852.0	319.20	1609.00	15968.0	31897	29988.00	3788.20	9739.0	1289	293.500	212.5	98.8	36.202	23.831	138.600	136.7	123	286.1	4598.80	502.3	3357.477	2994.6	20628	0.5695799	0.7240204
Liuyang	Changsha	40446	21415.0	43599.0	2473.10	4605.50	81113.0	63118	99254.00	23408.00	15719.0	6225	919.620	721.4	300.1	90.978	58.819	374.800	369.8	733	642.7	16233.00	1285.5	10844.470	26617.8	27345	0.4999611	0.7844544
Longhui	Shaoyang	33615	11925.0	8723.9	425.06	2741.60	10511.0	9572	9317.90	3985.50	3177.6	2726	709.990	604.4	436.7	95.163	54.211	344.600	298.8	85	834.1	2819.60	1098.2	4320.396	3264.6	12049	0.7595156	0.8512796
Longshan	Hunan West	34203	5557.0	2810.0	218.53	2052.40	4933.6	9754	893.45	2128.20	4164.0	1505	334.420	266.7	167.5	42.189	30.946	148.200	126.1	18	345.8	2293.90	508.3	2248.709	921.5	13138	0.6803069	0.7975001
Luxi	Hunan West	32680	2946.8	1772.0	184.25	1337.60	4878.3	17472	7085.60	1626.60	4089.1	664	197.490	149.7	80.9	21.683	17.160	82.400	71.1	42	174.3	917.41	280.3	1036.088	540.8	13247	0.6218337	0.7580131
Mayang	Huaihua	32772	3456.0	2703.1	215.86	1461.00	4738.8	13744	3876.90	2242.00	4299.8	975	216.850	160.0	148.1	24.173	15.207	90.300	87.8	33	245.0	1581.70	345.6	1865.938	5.2	14487	0.7089120	0.7378372
Miluo	Yueyang	36113	4749.3	15828.0	1068.60	2446.50	29548.0	42497	66342.00	3330.60	9421.3	965	451.270	303.3	162.8	40.221	30.662	204.900	193.6	269	351.4	5817.70	697.0	5688.717	8978.5	23379	0.5041607	0.6721032
Nan	Yiyang	35272	8921.7	3367.5	300.00	1987.10	15568.0	21311	11804.00	4928.10	8369.8	1877	366.100	325.6	226.1	35.487	29.444	259.200	201.3	91	455.9	5266.20	732.8	7783.359	6781.7	17691	0.6221343	0.8893745
Ningxiang	Changsha	40744	18662.0	49234.0	2448.90	4812.20	73250.0	62202	114145.00	18435.00	13763.0	4351	852.960	757.6	318.3	80.715	68.853	391.700	369.6	552	655.5	15623.00	1186.5	12804.480	18447.7	24020	0.5524652	0.8882011
Ningyuan	Yongzhou	34190	7351.4	7716.5	514.24	2234.40	8984.3	12697	5627.80	4249.40	4151.5	1753	444.920	401.3	157.8	68.336	32.471	185.500	157.8	64	460.9	3097.50	710.2	4283.431	9958.4	19742	0.6489721	0.9019599
Pingjiang	Yueyang	30017	8718.4	10627.0	461.62	2827.00	16444.0	17252	25647.00	5201.20	3780.8	2205	601.380	512.8	278.3	73.943	43.548	260.900	269.9	136	612.5	3448.30	957.5	5060.948	8789.3	14883	0.6396867	0.8527054
Qidong	Hengyang	30990	13633.0	6875.7	463.91	2413.20	17718.0	18001	26260.00	4246.10	9020.6	2055	607.640	529.2	311.0	80.694	51.474	289.200	287.3	115	627.8	6076.00	986.4	7380.180	15451.7	18256	0.6364558	0.8709104
Qiyang	Yongzhou	32059	14432.0	14439.0	499.51	2710.50	17705.0	20638	11567.00	6388.30	8816.0	2799	594.100	495.2	257.9	75.936	45.318	241.900	255.1	107	519.9	3832.70	860.7	6273.597	13568.8	19776	0.6040432	0.8335297
Rucheng	Chenzhou	35575	4777.6	3816.6	343.00	1492.70	3756.0	11286	4492.20	2426.20	2993.7	1130	232.280	197.3	127.8	33.101	14.478	111.300	101.6	43	235.7	751.80	333.2	2079.963	1744.7	13755	0.7073830	0.8494059
Sangzhi	Zhangjiajie	33916	3920.0	3081.3	248.06	1856.10	5615.4	14624	1694.80	2981.20	3405.9	1999	267.150	234.5	139.8	31.278	18.993	127.900	122.8	28	256.9	1803.30	385.5	3607.897	17585.8	45167	0.6664073	0.8777840
Shaodong	Shaoyang	31507	16184.0	12214.0	771.60	2757.00	22898.0	25246	29175.00	7855.30	10089.0	3080	724.310	547.7	310.0	99.082	59.009	363.200	297.8	148	524.9	8576.30	912.1	5704.602	4679.3	18296	0.5754851	0.7561679
Shaoshan	Xiangtan	33314	2626.4	4500.0	258.64	683.65	4956.8	55570	9717.60	1649.00	14916.0	488	73.652	62.0	33.6	5.910	3.201	27.147	30.4	48	57.7	1200.80	92.3	807.714	1630.3	24991	0.6251354	0.8417966
Shaoyang	Shaoyang	31783	8345.7	7237.3	376.42	2780.80	9031.2	9653	7887.80	2425.30	3499.3	2294	655.130	569.2	385.0	71.417	43.525	265.400	247.9	65	657.6	3406.30	942.3	5518.299	21656.5	65431	0.6978669	0.8688352
Shimen	Changde	33261	8334.4	10531.0	548.33	2178.80	16293.0	27137	17795.00	6026.50	6156.0	2502	392.050	329.6	193.8	29.245	26.104	190.600	184.7	122	399.2	6490.70	600.5	5266.510	6981.0	19275	0.6647794	0.8407091
Shuangfeng	Loudi	33684	11455.0	7904.9	470.59	2657.50	15225.0	17755	16665.00	3914.00	5470.3	1862	559.470	488.5	309.6	57.966	41.575	244.300	245.6	129	644.6	4596.00	859.4	7943.893	2613.1	14994	0.7500582	0.8731478
Shuangpai	Yongzhou	33302	1918.0	3572.0	226.37	881.96	3728.0	21942	2646.30	2056.40	4568.1	408	86.264	68.0	46.2	11.339	6.890	57.600	39.5	34	111.6	567.21	174.1	1866.171	9092.1	18479	0.6410109	0.7882778
Suining	Shaoyang	31750	4307.1	3605.6	222.40	1442.50	5658.1	16069	11150.00	1566.40	4990.4	802	264.080	208.9	145.2	26.200	14.261	108.800	86.3	54	268.4	1761.50	352.9	2064.499	1413.5	15004	0.7605554	0.7910482
Taojiang	Yiyang	35184	8657.4	8743.0	417.37	2276.80	15162.0	19509	18691.00	4656.80	8687.9	2504	472.800	411.4	194.0	48.047	33.234	260.900	208.8	153	504.5	5355.90	779.7	13878.842	13439.3	79214	0.6470437	0.8701354
Taoyuan	Changde	31877	11948.0	8656.0	710.08	2625.10	19603.0	22879	16529.00	4735.00	7682.6	2070	558.770	479.9	300.5	44.429	36.630	274.500	272.0	60	607.4	8926.00	857.1	18328.460	50619.0	60461	0.7086688	0.8588507
Tongdao	Huaihua	35400	2578.0	1525.4	165.59	1046.50	2653.2	12781	2514.50	1021.00	3696.4	882	144.490	105.5	82.2	15.913	7.776	57.900	49.7	27	154.2	749.14	208.1	981.418	644.2	12424	0.7409899	0.7301543
Wangcheng	Changsha	45171	12122.0	48829.0	2285.50	3802.30	37488.0	70666	148976.00	10330.00	16495.0	1678	361.480	268.6	131.2	28.838	24.815	161.300	154.8	314	266.6	5623.30	533.4	5222.356	6648.6	27690	0.4998125	0.7430563
Wugang	Shaoyang	30573	8618.0	7373.3	486.85	2346.00	9046.7	12112	5346.00	3852.00	4864.4	2250	483.620	402.5	271.4	70.758	43.683	243.900	194.0	52	502.9	3476.00	752.3	4613.704	1734.7	15126	0.6684833	0.8322650
Xiangtan	Xiangtan	35274	15516.0	10121.0	1236.60	3050.10	22728.0	27060	30730.00	12217.00	10135.0	2022	610.490	551.9	347.1	46.556	54.439	248.590	239.1	187	574.0	4889.10	845.2	10688.618	40758.0	69261	0.6791292	0.9040279
Xiangxiang	Xiangtan	33040	13298.0	9819.0	975.59	2942.80	23175.0	29361	39630.00	7900.30	9264.3	2451	586.400	492.0	324.5	47.743	39.612	231.710	242.0	189	535.7	5891.80	787.8	6852.943	17531.9	22297	0.6799949	0.8390177
Xiangyin	Yueyang	33169	5466.1	14714.0	520.53	2318.80	23265.0	33983	49507.00	5222.90	8824.5	1550	466.110	357.4	169.4	44.878	30.752	193.800	190.1	152	408.4	4273.20	686.9	6000.857	8175.0	19945	0.5945552	0.7667718
Xinhua	Loudi	32496	11075.0	6725.3	576.47	3599.50	14940.0	13398	12152.00	6121.20	3342.4	1542	755.140	677.9	451.6	96.224	57.670	316.600	313.8	112	817.4	5743.50	1116.7	6919.849	3145.3	13834	0.7319782	0.8977143
Xinhuang	Huaihua	31891	2373.1	2075.8	170.11	1069.30	3782.1	15412	3405.70	1265.20	3935.6	1350	149.710	105.6	104.0	15.938	8.781	72.000	72.5	36	178.6	873.45	246.0	1130.322	785.8	12732	0.7260163	0.7053637
Xinning	Shaoyang	32067	6126.3	5978.8	390.67	1830.60	6064.6	10732	3857.70	2899.90	3287.7	1565	429.840	347.8	227.4	41.633	22.005	171.400	146.5	38	383.6	1445.90	566.7	2415.712	2364.9	13031	0.6769014	0.8091383
Xinshao	Shaoyang	34199	7344.2	8313.8	384.19	2229.20	8590.9	11514	10829.00	5042.50	3986.4	2319	577.690	477.4	265.8	68.131	39.034	234.100	213.0	79	533.6	2941.60	749.0	3003.553	5679.2	13778	0.7124166	0.8263948
Xintian	Yongzhou	33609	3851.6	3401.9	250.31	1280.20	4776.4	14426	3357.40	1334.90	2894.9	1264	236.520	217.1	116.9	32.138	15.970	93.800	107.1	42	226.6	1329.80	332.1	2530.482	3134.3	16925	0.6823246	0.9178928
Xupu	Huaihua	29873	8675.5	6112.2	457.86	2452.00	10314.0	13863	6720.40	4588.00	5453.1	2106	512.610	400.9	292.3	53.793	29.166	226.100	211.2	71	516.0	3427.30	745.9	4308.431	242.6	16558	0.6917817	0.7820760
Yanling	Zhuzhou	34156	3274.4	5835.0	402.90	1038.20	4250.5	21021	5855.80	2379.60	3608.4	545	116.180	99.0	54.0	10.838	6.682	52.200	46.0	75	112.2	1241.20	202.2	971.500	6851.0	18652	0.5548961	0.8521260
Yizhang	Chenzhou	33508	7938.8	9992.5	750.40	2142.60	10455.0	17814	19120.00	3697.00	3788.6	2280	348.830	279.9	128.8	63.564	25.843	161.300	142.5	169	363.4	5037.50	588.9	2521.831	3584.6	19318	0.6170827	0.8023966
Yongshun	Hunan West	31234	4516.9	2464.1	220.66	2021.70	4142.1	9590	1061.00	2839.90	3963.1	1801	312.990	259.4	195.7	38.686	24.854	115.700	113.9	23	292.5	2247.30	433.3	2018.756	845.8	12650	0.6750519	0.8287805
Yongxing	Chenzhou	33278	7097.6	13456.0	1294.50	2476.00	21382.0	37651	43700.00	3053.70	9856.1	1969	375.500	304.9	133.5	52.440	19.765	172.500	145.7	175	333.5	4807.10	562.6	3174.984	4540.5	19960	0.5927835	0.8119840
You	Zhuzhou	36791	9541.6	15611.0	1533.30	2803.00	25153.0	36264	32738.00	6316.20	13021.0	1992	472.320	418.0	254.3	42.124	31.908	186.400	196.9	248	344.4	7654.80	693.7	6071.620	27443.0	22732	0.4964682	0.8849932
Yuanjiang	Yiyang	33302	7763.4	10486.0	509.45	2381.20	17603.0	26258	21082.00	6464.20	10060.0	1856	401.220	335.2	203.3	34.220	27.932	260.300	161.0	105	366.7	5125.10	672.5	6644.520	5899.6	20552	0.5452788	0.8354519
Yuanling	Huaihua	37762	5627.0	5466.8	677.40	2202.60	14156.0	24194	14835.00	2485.30	4265.4	2501	382.530	283.9	210.2	33.935	21.278	166.500	155.9	56	397.0	3092.50	586.5	2508.387	637.8	15165	0.6768968	0.7421640
Yueyang	Yueyang	31470	4946.6	15084.0	330.43	1971.60	18974.0	26360	36800.00	3668.70	10377.0	1616	411.260	293.3	173.0	40.218	30.051	201.500	150.9	158	435.3	5836.60	721.7	11279.478	15381.2	88494	0.6031592	0.7131741
Zhijiang	Huaihua	33582	4306.1	2802.2	356.96	1470.00	6992.5	20518	4491.80	2477.30	4535.1	935	223.750	175.5	116.1	23.693	14.726	101.800	94.3	56	247.6	2133.30	341.6	2576.470	90.8	13589	0.7248244	0.7843575
Zhongfang	Huaihua	34941	1296.3	7594.6	348.83	1048.00	7332.1	30846	8608.50	968.44	6082.5	662	170.250	103.1	89.3	12.709	8.563	71.100	70.9	56	173.8	1064.90	238.3	2917.158	1938.6	37231	0.7293328	0.6055800
Zhuzhou	Zhuzhou	37191	5395.6	4777.7	507.04	1408.80	7962.1	27589	6768.90	2970.20	11407.0	1032	210.380	177.0	106.0	12.436	11.824	92.200	85.2	82	210.6	2538.40	289.6	4236.370	10883.0	103228	0.7272099	0.8413347
Zixing	Chenzhou	34163	7873.2	14891.0	1556.00	2679.00	22261.0	65706	51921.00	5014.70	10838.0	1159	261.980	177.9	76.0	22.316	14.760	114.000	86.3	155	140.2	4835.80	340.2	2761.164	3636.3	21600	0.4121105	0.6790595

Performing relational join

The code chunk below will be used to update the attribute table of hunan’s SpatialPolygonsDataFrame with the attribute fields of hunan2012 dataframe. This is performed by using left_join() of dplyr package.

colnames(hunan)

[1] "NAME_2"     "ID_3"       "NAME_3"     "ENGTYPE_3"  "Shape_Leng"
[6] "Shape_Area" "County"     "geometry"  

colnames(hunan2012)

 [1] "County"      "City"        "avg_wage"    "deposite"    "FAI"        
 [6] "Gov_Rev"     "Gov_Exp"     "GDP"         "GDPPC"       "GIO"        
[11] "Loan"        "NIPCR"       "Bed"         "Emp"         "EmpR"       
[16] "EmpRT"       "Pri_Stu"     "Sec_Stu"     "Household"   "Household_R"
[21] "NOIP"        "Pop_R"       "RSCG"        "Pop_T"       "Agri"       
[26] "Service"     "Disp_Inc"    "RORP"        "ROREmp"     

hunan <- left_join(hunan,hunan2012) %>%
  select(1:4, 7, 15)

3.2 Visualising Regional Development Indicator

Now, we are going to prepare a basemap and a choropleth map showing the distribution of GDPPC 2012 by using qtm() of tmap package.

Show the code

basemap <- tm_shape(hunan) +
  tm_polygons() +
  tm_text("NAME_3", 
          size=0.3) +
  tm_layout(bg.color = "#E4D5C9",
            frame = F)

gdppc <- qtm(hunan, "GDPPC") +
  tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 0.9,
            legend.text.size = 0.5)

tmap_arrange(basemap, gdppc, asp=1, ncol=2)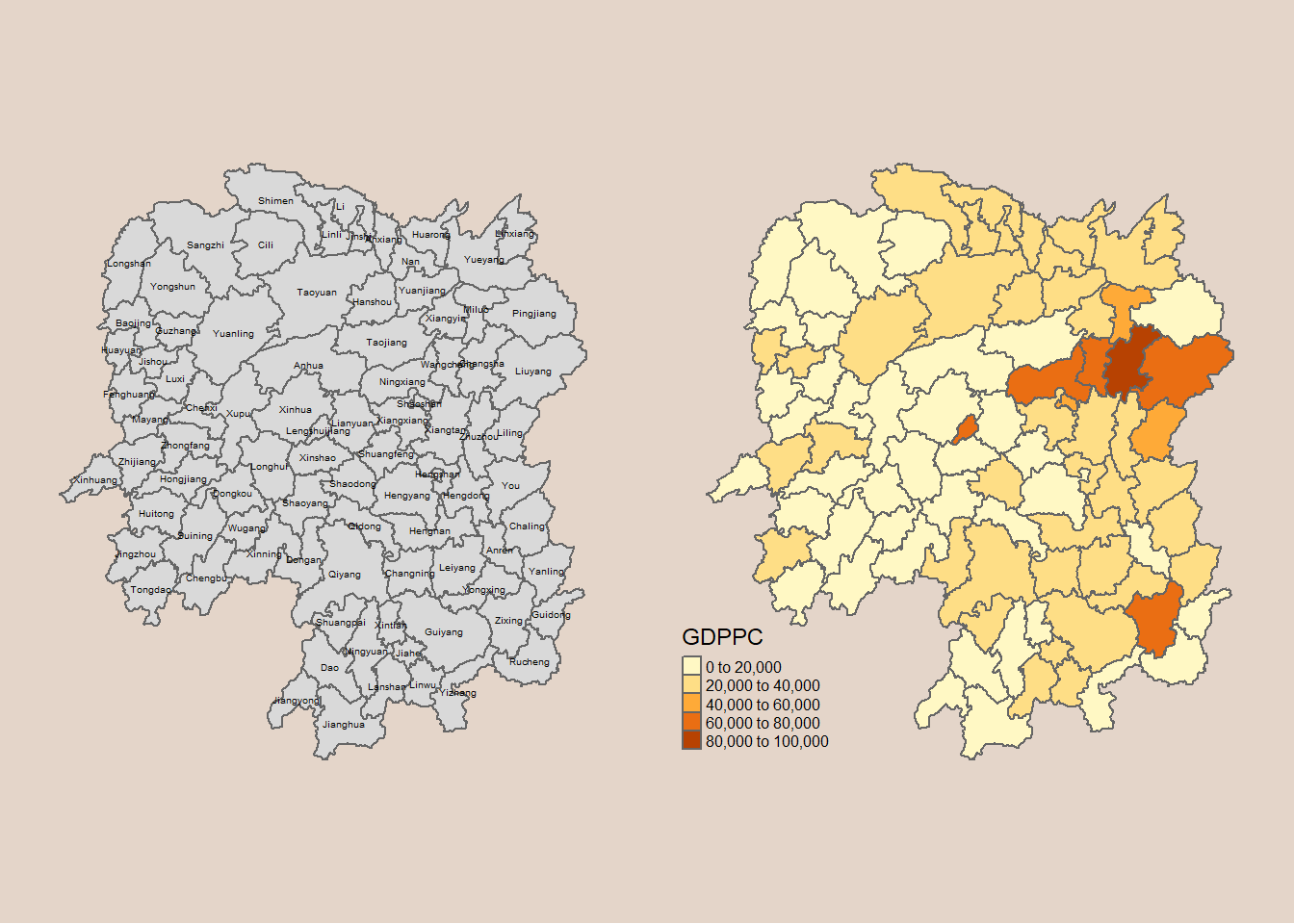

4 Local Indicatros of Spatial Association

• Local Indicators of Spatial Association (LISA): statistics that evaluate the existence of clusters in the spatial arrangement of a given variable.

• Eg if we are studying cancer rates among census tracts in a given city local clusters in the rates mean that there are areas that have higher or lower rates than is to be expected by chance alone; that is, the values occurring are above or below those of a random distribution in space.

In this section, we learn how to apply appropriate Local Indicators for Spatial Association (LISA), especially local Moran’s I to detect cluster and/or outlier from GDP per capita 2012 of Hunan Province, PRC.

4.1 Computing Contiguity Spatial Weights

Before we can compute the global spatial autocorrelation statistics, we need to construct a spatial weights of the study area. The spatial weights is used to define the neighbourhood relationships between the geographical units (i.e. county) in the study area.

• poly2nb() of spdep package to compute contiguity weight matrices for the study area.
• This function builds a neighbours list based on regions with contiguous boundaries. If you look at the documentation you will see that you can pass a “queen” argument that takes TRUE or FALSE as options.
• Default: Queen = TRUE, but if you change it to FALSE, you are using ROOK method.
• The output that you will get is a list.

The code chunk below will be used to compute Queen contiguity weight matrix:

wm_q <- poly2nb(hunan, 
                queen=TRUE)
summary(wm_q)

Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 
Link number distribution:

 1  2  3  4  5  6  7  8  9 11 
 2  2 12 16 24 14 11  4  2  1 
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 11 links

Interpretation

• There are 88 area units in Hunan.
• Most connected area unit has 11 neighbours.
• There are 2 area units with only 1 neighbour.

4.2 Row-standardised weights matrix

• Assign weights to each neighboring polygon. In our case, each neighboring polygon will be assigned equal weight (style=“W”).

• This is accomplished by assigning the fraction 1/(# of neighbors) to each neighboring county then summing the weighted income values.

• While this is the most intuitive way to summaries the neighbors’ values it has one drawback in that polygons along the edges of the study area will base their lagged values on fewer polygons thus potentially over- or under-estimating the true nature of the spatial autocorrelation in the data.

• Style=“W” option used for this example for simplicity’s sake but more robust options are available, notably style=“B”.

  • Styles:
    • W: row standardised (sums over all links to n)
    • B: basic binary coding
    • C: globally standardised (sums over all links to n)
    • U: equal to C divided by the number of neighbours (sums over all links to unity)
    • S: variance-stabilizing coding scheme (sums over all links to n)
    • minmax: divides the weights by min of the max row sums and max column sums of the input weights; similar to C/U

• The input of *nb2listw() must be an object of class nb. The syntax of the function has two major arguments, namely style and zero.poly.

rswm_q <- nb2listw(wm_q,
                   style="W",
                   zero.policy = TRUE) 
rswm_q

Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 

Weights style: W 
Weights constants summary:
   n   nn S0       S1       S2
W 88 7744 88 37.86334 365.9147

zero.policy = TRUE allows for lists of non-neighbors. This should be used with caution since the user may not be aware of missing neighbors in their dataset however, a zero.policy = FALSE would return an error.

If zero policy = TRUE, weights vectors of zero length are inserted for regions without neighbour in the neighbours list. These will in turn generate lag values of zero, equivalent to the sum of products of the zero row t(rep(0, length = length(neighbours))) %*% x, for arbitrary numerical vector x of length length(neighbours). The spatially lagged value of x for the zero-neighbour region will then be zero, which may (or may not) be a sensible choice.

4.3 Computing Local Moran’s I

localmoran() function of spdep computes \(I_i\) values, given a set of \(z_i\) values and a listw object providing neighbour weighting information for the polygon associated with the zi values

The code chunks below are used to compute local Moran’s I of GDPPC2012 at the county level.

fips <- order(hunan$County)
localMI <- localmoran(hunan$GDPPC, rswm_q)

head(localMI,10) %>% 
  kable() %>% 
  kableExtra::kable_styling(bootstrap_options = c("striped", "hover", "condensed", "responsive"),
                            fixed_thead = T)

Ii	E.Ii	Var.Ii	Z.Ii	Pr(z != E(Ii))
-0.0014685	-0.0000282	0.0004724	-0.0662690	0.9471636
0.0258782	-0.0006062	0.0101666	0.2626643	0.7928094
-0.0119876	-0.0053666	0.1133362	-0.0196670	0.9843090
0.0010225	-0.0000002	0.0000051	0.4525980	0.6508382
0.0148149	-0.0000683	0.0014499	0.3908581	0.6959021
-0.0387938	-0.0003860	0.0064756	-0.4772884	0.6331568
3.3688217	-0.0775018	1.5180283	2.7971523	0.0051555
1.5606896	-0.0738777	0.8001247	1.8273593	0.0676458
4.4219586	-0.1106694	1.3595930	3.8872782	0.0001014
-0.3993226	-0.0070111	0.0703477	-1.4791294	0.1391057

• Ii: the local Moran’s I statistics
• E.Ii: the expectation of local moran statistic under the randomisation hypothesis
• Var.Ii: the variance of local moran statistic under the randomisation hypothesis
• Z.Ii:the standard deviate of local moran statistic
• Pr(): the p-value of local moran statistic

The code chunk below list the content of the local Moran matrix derived by using printCoefmat().

printCoefmat(data.frame(
  localMI[fips,], 
  row.names=hunan$County[fips]),
  check.names=FALSE)

                       Ii        E.Ii      Var.Ii        Z.Ii Pr.z....E.Ii..
Anhua         -2.2493e-02 -5.0048e-03  5.8235e-02 -7.2467e-02         0.9422
Anren         -3.9932e-01 -7.0111e-03  7.0348e-02 -1.4791e+00         0.1391
Anxiang       -1.4685e-03 -2.8150e-05  4.7238e-04 -6.6269e-02         0.9472
Baojing        3.4737e-01 -5.0089e-03  8.3636e-02  1.2185e+00         0.2230
Chaling        2.0559e-02 -9.6812e-04  2.7711e-02  1.2932e-01         0.8971
Changning     -2.9868e-05 -9.0010e-09  1.5105e-07 -7.6828e-02         0.9388
Changsha       4.9022e+00 -2.1348e-01  2.3194e+00  3.3590e+00         0.0008
Chengbu        7.3725e-01 -1.0534e-02  2.2132e-01  1.5895e+00         0.1119
Chenxi         1.4544e-01 -2.8156e-03  4.7116e-02  6.8299e-01         0.4946
Cili           7.3176e-02 -1.6747e-03  4.7902e-02  3.4200e-01         0.7324
Dao            2.1420e-01 -2.0824e-03  4.4123e-02  1.0297e+00         0.3032
Dongan         1.5210e-01 -6.3485e-04  1.3471e-02  1.3159e+00         0.1882
Dongkou        5.2918e-01 -6.4461e-03  1.0748e-01  1.6338e+00         0.1023
Fenghuang      1.8013e-01 -6.2832e-03  1.3257e-01  5.1198e-01         0.6087
Guidong       -5.9160e-01 -1.3086e-02  3.7003e-01 -9.5104e-01         0.3416
Guiyang        1.8240e-01 -3.6908e-03  3.2610e-02  1.0305e+00         0.3028
Guzhang        2.8466e-01 -8.5054e-03  1.4152e-01  7.7931e-01         0.4358
Hanshou        2.5878e-02 -6.0620e-04  1.0167e-02  2.6266e-01         0.7928
Hengdong       9.9964e-03 -4.9063e-04  6.7742e-03  1.2742e-01         0.8986
Hengnan        2.8064e-02 -3.2160e-04  3.7597e-03  4.6294e-01         0.6434
Hengshan      -5.8201e-03 -3.0437e-05  5.1076e-04 -2.5618e-01         0.7978
Hengyang       6.2997e-02 -1.3046e-03  2.1865e-02  4.3486e-01         0.6637
Hongjiang      1.8790e-01 -2.3019e-03  3.1725e-02  1.0678e+00         0.2856
Huarong       -1.5389e-02 -1.8667e-03  8.1030e-02 -4.7503e-02         0.9621
Huayuan        8.3772e-02 -8.5569e-04  2.4495e-02  5.4072e-01         0.5887
Huitong        2.5997e-01 -5.2447e-03  1.1077e-01  7.9685e-01         0.4255
Jiahe         -1.2431e-01 -3.0550e-03  5.1111e-02 -5.3633e-01         0.5917
Jianghua       2.8651e-01 -3.8280e-03  8.0968e-02  1.0204e+00         0.3076
Jiangyong      2.4337e-01 -2.7082e-03  1.1746e-01  7.1800e-01         0.4728
Jingzhou       1.8270e-01 -8.5106e-04  2.4363e-02  1.1759e+00         0.2396
Jinshi        -1.1988e-02 -5.3666e-03  1.1334e-01 -1.9667e-02         0.9843
Jishou        -2.8680e-01 -2.6305e-03  4.4028e-02 -1.3543e+00         0.1756
Lanshan        6.3334e-02 -9.6365e-04  2.0441e-02  4.4972e-01         0.6529
Leiyang        1.1581e-02 -1.4948e-04  2.5082e-03  2.3422e-01         0.8148
Lengshuijiang -1.7903e+00 -8.2129e-02  2.1598e+00 -1.1623e+00         0.2451
Li             1.0225e-03 -2.4048e-07  5.1060e-06  4.5260e-01         0.6508
Lianyuan      -1.4672e-01 -1.8983e-03  1.9145e-02 -1.0467e+00         0.2952
Liling         1.3774e+00 -1.5097e-02  4.2601e-01  2.1335e+00         0.0329
Linli          1.4815e-02 -6.8294e-05  1.4499e-03  3.9086e-01         0.6959
Linwu         -2.4621e-03 -9.0703e-06  1.9258e-04 -1.7676e-01         0.8597
Linxiang       6.5904e-02 -2.9028e-03  2.5470e-01  1.3634e-01         0.8916
Liuyang        3.3688e+00 -7.7502e-02  1.5180e+00  2.7972e+00         0.0052
Longhui        8.0801e-01 -1.1377e-02  1.5538e-01  2.0787e+00         0.0376
Longshan       7.5663e-01 -1.1100e-02  3.1449e-01  1.3690e+00         0.1710
Luxi           1.8177e-01 -2.4855e-03  3.4249e-02  9.9561e-01         0.3194
Mayang         2.1852e-01 -5.8773e-03  9.8049e-02  7.1663e-01         0.4736
Miluo          1.8704e+00 -1.6927e-02  2.7925e-01  3.5715e+00         0.0004
Nan           -9.5789e-03 -4.9497e-04  6.8341e-03 -1.0988e-01         0.9125
Ningxiang      1.5607e+00 -7.3878e-02  8.0012e-01  1.8274e+00         0.0676
Ningyuan       2.0910e-01 -7.0884e-03  8.2306e-02  7.5356e-01         0.4511
Pingjiang     -9.8964e-01 -2.6457e-03  5.6027e-02 -4.1698e+00         0.0000
Qidong         1.1806e-01 -2.1207e-03  2.4747e-02  7.6396e-01         0.4449
Qiyang         6.1966e-02 -7.3374e-04  8.5743e-03  6.7712e-01         0.4983
Rucheng       -3.6992e-01 -8.8999e-03  2.5272e-01 -7.1814e-01         0.4727
Sangzhi        2.5053e-01 -4.9470e-03  6.8000e-02  9.7972e-01         0.3272
Shaodong      -3.2659e-02 -3.6592e-05  5.0546e-04 -1.4510e+00         0.1468
Shaoshan       2.1223e+00 -5.0227e-02  1.3668e+00  1.8583e+00         0.0631
Shaoyang       5.9499e-01 -1.1253e-02  1.3012e-01  1.6807e+00         0.0928
Shimen        -3.8794e-02 -3.8603e-04  6.4756e-03 -4.7729e-01         0.6332
Shuangfeng     9.2835e-03 -2.2867e-03  3.1516e-02  6.5174e-02         0.9480
Shuangpai      8.0591e-02 -3.1366e-04  8.9838e-03  8.5358e-01         0.3933
Suining        3.7585e-01 -3.5933e-03  4.1870e-02  1.8544e+00         0.0637
Taojiang      -2.5394e-01 -1.2395e-03  1.4477e-02 -2.1002e+00         0.0357
Taoyuan        1.4729e-02 -1.2039e-04  8.5103e-04  5.0903e-01         0.6107
Tongdao        4.6482e-01 -6.9870e-03  1.9879e-01  1.0582e+00         0.2900
Wangcheng      4.4220e+00 -1.1067e-01  1.3596e+00  3.8873e+00         0.0001
Wugang         7.1003e-01 -7.8144e-03  1.0710e-01  2.1935e+00         0.0283
Xiangtan       2.4530e-01 -3.6457e-04  3.2319e-03  4.3213e+00         0.0000
Xiangxiang     2.6271e-01 -1.2703e-03  2.1290e-02  1.8092e+00         0.0704
Xiangyin       5.4525e-01 -4.7442e-03  7.9236e-02  1.9539e+00         0.0507
Xinhua         1.1810e-01 -6.2649e-03  8.6001e-02  4.2409e-01         0.6715
Xinhuang       1.5725e-01 -4.1820e-03  3.6648e-01  2.6667e-01         0.7897
Xinning        6.8928e-01 -9.6674e-03  2.0328e-01  1.5502e+00         0.1211
Xinshao        5.7578e-02 -8.5932e-03  1.1769e-01  1.9289e-01         0.8470
Xintian       -7.4050e-03 -5.1493e-03  1.0877e-01 -6.8395e-03         0.9945
Xupu           3.2406e-01 -5.7468e-03  5.7735e-02  1.3726e+00         0.1699
Yanling       -6.9021e-02 -5.9211e-04  9.9306e-03 -6.8667e-01         0.4923
Yizhang       -2.6844e-01 -2.2463e-03  4.7588e-02 -1.2202e+00         0.2224
Yongshun       6.3064e-01 -1.1350e-02  1.8830e-01  1.4795e+00         0.1390
Yongxing       4.3411e-01 -9.0735e-03  1.5088e-01  1.1409e+00         0.2539
You            7.8750e-02 -7.2728e-03  1.2116e-01  2.4714e-01         0.8048
Yuanjiang      2.0004e-04 -1.7760e-04  2.9798e-03  6.9181e-03         0.9945
Yuanling       8.7298e-03 -2.2981e-06  2.3221e-05  1.8121e+00         0.0700
Yueyang        4.1189e-02 -1.9768e-04  2.3113e-03  8.6085e-01         0.3893
Zhijiang       1.0476e-01 -7.8123e-04  1.3100e-02  9.2214e-01         0.3565
Zhongfang     -2.2685e-01 -2.1455e-03  3.5927e-02 -1.1855e+00         0.2358
Zhuzhou        3.2864e-01 -5.2432e-04  7.2391e-03  3.8688e+00         0.0001
Zixing        -7.6849e-01 -8.8210e-02  9.4057e-01 -7.0144e-01         0.4830

4.3.1 Mapping the Local Moran’s I

• Before mapping the local Moran’s I map, it is wise to append the local Moran’s I dataframe (i.e. localMI) onto hunan SpatialPolygonDataFrame.
• The output SpatialPolygonDataFrame is called hunan.localMI
• The code chunks below can be used to perform the task.

hunan.localMI <- cbind(hunan,localMI) %>%
  rename(Pr.Ii = Pr.z....E.Ii..)

hunan.localMI

Simple feature collection with 88 features and 11 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84
First 10 features:
     NAME_2  ID_3    NAME_3   ENGTYPE_3    County GDPPC           Ii
1   Changde 21098   Anxiang      County   Anxiang 23667 -0.001468468
2   Changde 21100   Hanshou      County   Hanshou 20981  0.025878173
3   Changde 21101    Jinshi County City    Jinshi 34592 -0.011987646
4   Changde 21102        Li      County        Li 24473  0.001022468
5   Changde 21103     Linli      County     Linli 25554  0.014814881
6   Changde 21104    Shimen      County    Shimen 27137 -0.038793829
7  Changsha 21109   Liuyang County City   Liuyang 63118  3.368821673
8  Changsha 21110 Ningxiang      County Ningxiang 62202  1.560689600
9  Changsha 21111 Wangcheng      County Wangcheng 70666  4.421958618
10 Chenzhou 21112     Anren      County     Anren 12761 -0.399322576
            E.Ii       Var.Ii        Z.Ii        Pr.Ii
1  -2.815006e-05 4.723841e-04 -0.06626904 0.9471636332
2  -6.061953e-04 1.016664e-02  0.26266425 0.7928093714
3  -5.366648e-03 1.133362e-01 -0.01966705 0.9843089778
4  -2.404783e-07 5.105969e-06  0.45259801 0.6508382339
5  -6.829362e-05 1.449949e-03  0.39085814 0.6959020959
6  -3.860263e-04 6.475559e-03 -0.47728835 0.6331568039
7  -7.750185e-02 1.518028e+00  2.79715225 0.0051555232
8  -7.387766e-02 8.001247e-01  1.82735933 0.0676457604
9  -1.106694e-01 1.359593e+00  3.88727819 0.0001013746
10 -7.011066e-03 7.034768e-02 -1.47912938 0.1391057404
                         geometry
1  POLYGON ((112.0625 29.75523...
2  POLYGON ((112.2288 29.11684...
3  POLYGON ((111.8927 29.6013,...
4  POLYGON ((111.3731 29.94649...
5  POLYGON ((111.6324 29.76288...
6  POLYGON ((110.8825 30.11675...
7  POLYGON ((113.9905 28.5682,...
8  POLYGON ((112.7181 28.38299...
9  POLYGON ((112.7914 28.52688...
10 POLYGON ((113.1757 26.82734...

4.3.2 Mapping local Moran’s I values

Plot the local Moran’s I values by using choropleth mapping functions of tmap package.

Show the code

tm_shape(hunan.localMI) +
  tm_fill(col = "Ii", 
          style = "pretty",
          palette = "RdBu",
          title = "local moran statistics") +
  tm_borders(alpha = 0.5) +
  tm_layout(bg.color = "#E4D5C9",
            frame = F)

4.3.3 Mapping Local Moran’s I p-values

For effective interpretation, it is better to plot both the local Moran’s I values map and its corresponding p-values map next to each other.

Show the code

tm_shape(hunan.localMI) +
  tm_fill(col = "Pr.Ii", 
          breaks=c(-Inf, 0.001, 0.01, 0.05, 0.1, Inf),
          palette="-Blues", 
          title = "local Moran's I p-values") +
  tm_borders(alpha = 0.5)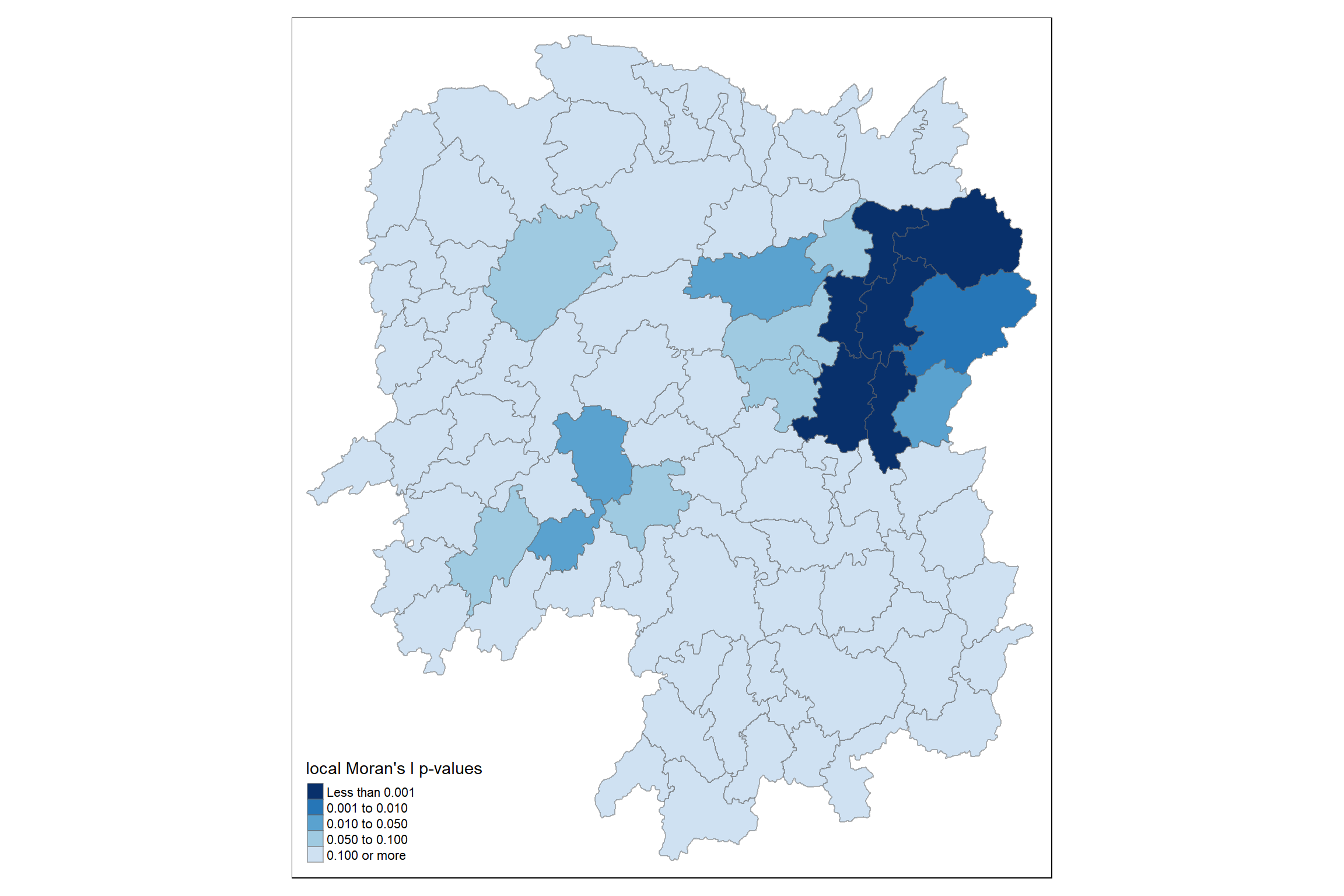

Mapping both Local Moran’s I values and p-values

Plot both the local Moran’s I values map and its corresponding p-values map next to each other for easier comparison.

localMI.map <- tm_shape(hunan.localMI) +
  tm_fill(col = "Ii", #<<
          style = "pretty", 
          title = "local moran statistics") +
  tm_borders(alpha = 0.5)+
  tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 0.9,
            legend.text.size = 0.8)

pvalue.map <- tm_shape(hunan.localMI) +
  tm_fill(col = "Pr.Ii", #<<
          breaks=c(-Inf, 0.001, 0.01, 0.05, 0.1, Inf),
          palette="-Blues", 
          title = "local Moran's I p-values") +
  tm_borders(alpha = 0.5) +
  tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 0.9,
            legend.text.size = 0.8)

tmap_arrange(localMI.map, pvalue.map, asp=1, ncol=2)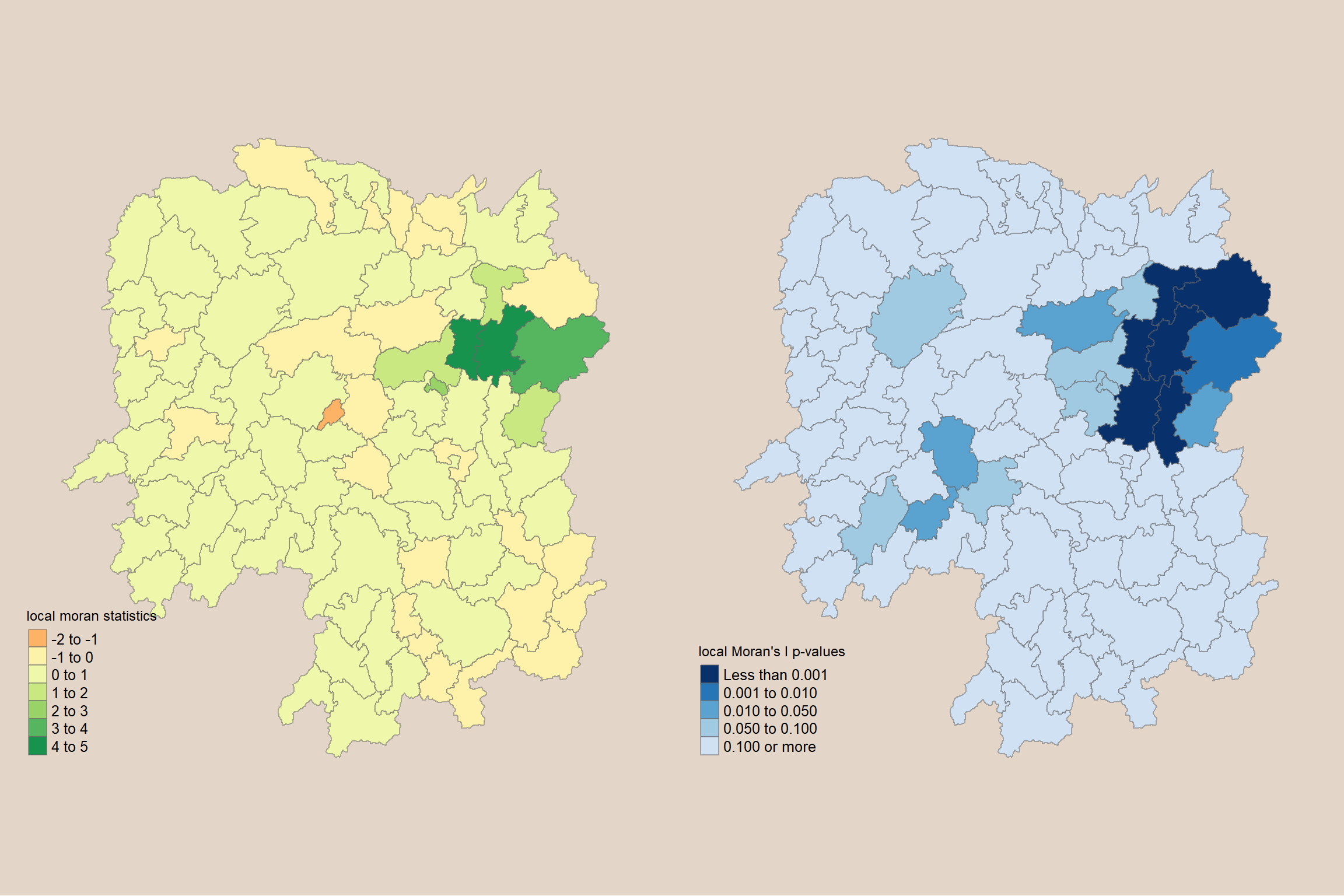

• You need to plot it together to draw any conclusions
• Then we need to decompose these relationshops using LISA Cluster

5 Creating a LISA Cluster Map

The LISA Cluster Map shows the significant locations color coded by type of spatial autocorrelation. The first step before we can generate the LISA cluster map is to plot the Moran scatterplot.

5.1 Plotting Moran scatterplot

The Moran scatterplot is an illustration of the relationship between the values of the chosen attribute at each location and the average value of the same attribute at neighboring locations.

The code chunk below plots the Moran scatterplot of GDPPC 2012 by using moran.plot() of spdep.

par(bg = '#E4D5C9')

nci <- moran.plot(hunan$GDPPC, rswm_q,
                  labels=as.character(hunan$County),
                  xlab="GDPPC 2012", 
                  ylab="Spatially Lag GDPPC 2012")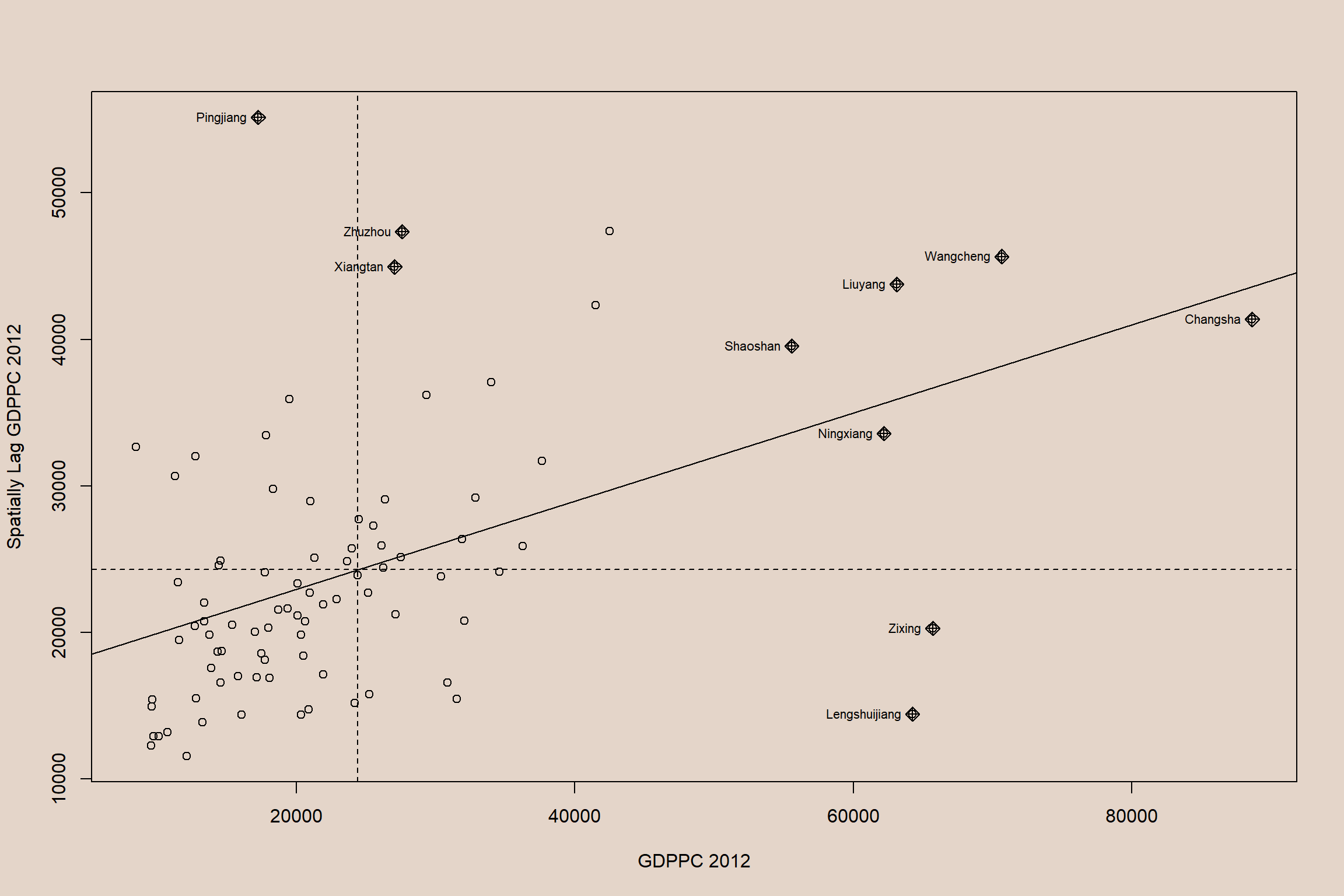

Interpretation

• Plot is split in 4 quadrants.
  • LH (Neg- ac, Outlier), HH (Pos+ ac, Cluster)
  • LL (Pos+ ac, Cluster), HL (Neg- ac, Outlier)
  • Wz is neighbour (y axis), z is you/target (x axis)
• For this plot, you need to standardise it by scaling it and have both to cutoff at 0.
• The top right corner belongs to areas that have high GDPPC and are surrounded by other areas that have the average level of GDPPC.
  • This are the high-high locations in the lesson slide: “I’m high and my neighbours are high.”

5.2 Plotting Moran scatterplot with standardised variable

• Use scale() to centers and scales the variable.
• Here, centering is done by subtracting the mean (omitting NAs) the corresponding columns,
• and scaling is done by dividing the (centered) variable by their standard deviations.
• The as.vector() added to the end is to make sure that the data type we get out of this is a vector, that map neatly into out dataframe.

hunan$Z.GDPPC <- scale(hunan$GDPPC) %>% 
  as.vector 

Plot the Moran scatterplot again by using the code chunk below.

par(bg = '#E4D5C9')

nci2 <- moran.plot(hunan$Z.GDPPC, rswm_q,
                   labels=as.character(hunan$County),
                   xlab="z-GDPPC 2012", 
                   ylab="Spatially Lag z-GDPPC 2012")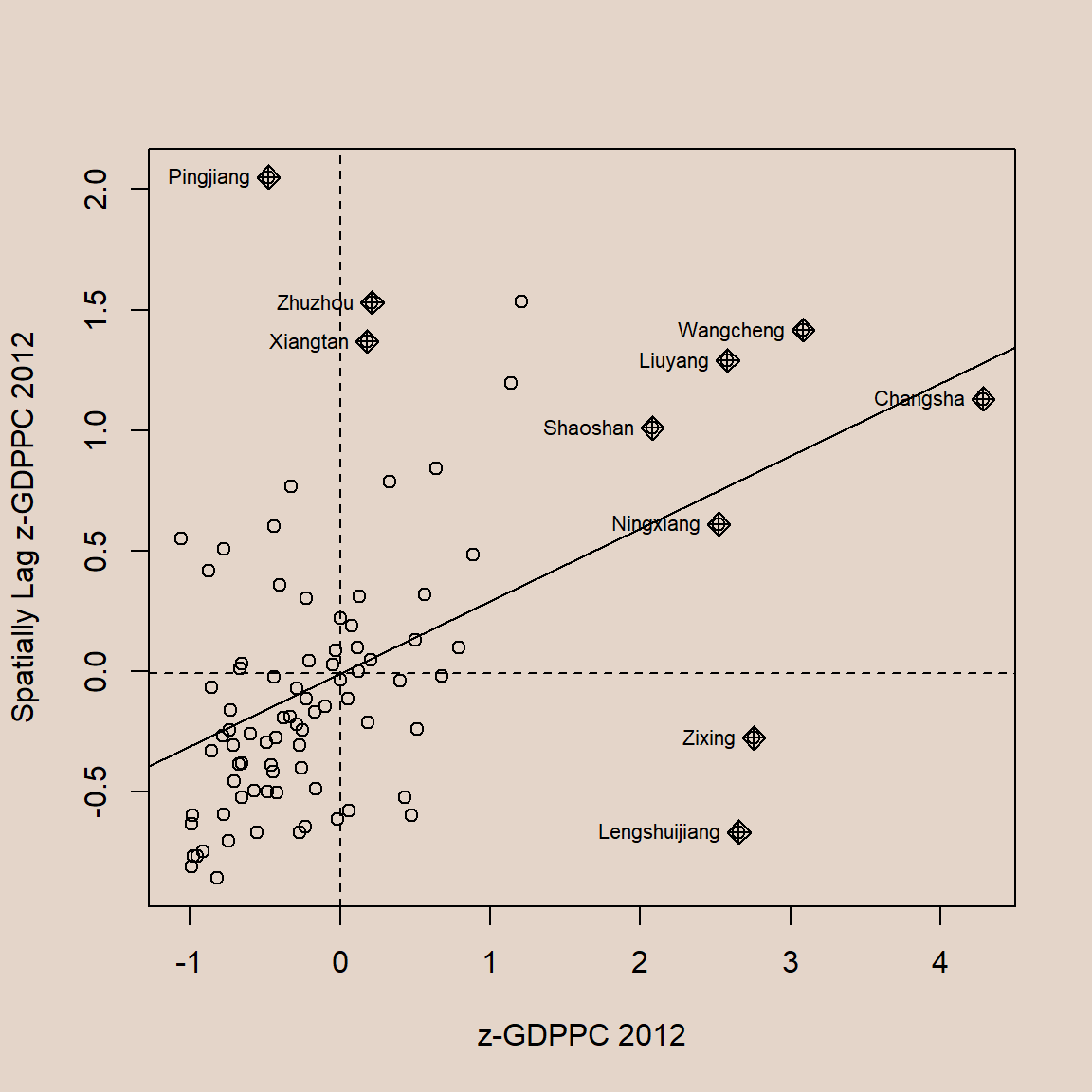

Interpretation

• Plot is split in 4 quadrants.
  • LH (Neg- ac, Outlier), HH (Pos+ ac, cluster)
  • LL (Pos+ ac, Cluster), HL (Neg- ac, outlier)
  • Wz is neighbour (y axis), z is you/target (x axis)
• After scaling it, we can see that both is now cutoff at 0.

5.3 Preparing LISA map classes

5.3.1 Convert to Vector

The code chunks below show the steps to prepare a LISA cluster map.

quadrant <- vector(mode="numeric",
                   length=nrow(localMI))

5.3.2 Derive spatially lagged GDPPC

Next, derive the spatially lagged variable of interest (i.e. GDPPC) and centers the spatially lagged variable around its mean.

hunan$lag_GDPPC <- lag.listw(rswm_q, 
                             hunan$GDPPC)

DV <- hunan$lag_GDPPC - mean(hunan$lag_GDPPC)     

5.3.3 Center variable around mean

This is follow by centering the local Moran’s around the mean.

LM_I <- localMI[,1] - mean(localMI[,1])    

5.3.4 Set alpha value

Next, we will set a statistical significance level for the local Moran.

signif <- 0.05       

5.3.5 Define quadrants

These four command lines define the low-low (1), low-high (2), high-low (3) and high-high (4) categories.

quadrant[DV <0 & LM_I>0] <- 1
quadrant[DV >0 & LM_I<0] <- 2
quadrant[DV <0 & LM_I<0] <- 3  
quadrant[DV >0 & LM_I>0] <- 4      

5.3.6 Place Moran

Lastly, place non-significant Moran in the category 0.

quadrant[localMI[,5]>signif] <- 0

5.4 Plotting LISA map

5.4.1 LISA Map

Now, we can build the LISA map by using the code chunks below.

hunan.localMI$quadrant <- quadrant
colors <- c("#eeeae2", "#2c7bb6", "#abd9e9", "#fdae61", "#d7191c")
clusters <- c("insignificant", "low-low", "low-high", "high-low", "high-high")

tm_shape(hunan.localMI) +
  tm_fill(col = "quadrant", 
          style = "cat", 
          palette = colors[c(sort(unique(quadrant)))+1], 
          labels = clusters[c(sort(unique(quadrant)))+1],
          popup.vars = c("")) +
  tm_view(set.zoom.limits = c(11,17)) +
  tm_borders(alpha=0.5) +
  tm_layout(bg.color = "#E4D5C9",
            frame = F)

Quadrants

• High-High (Cluster): counties that have High GDPPC surrounded by counties with High GDPPC
• High-Low (Outlier): counties that have High GDPPC surrounded by counties with Low GDPPC
• Low-High (Outlier): counties that have low GDPPC surrounded by counties with High GDPPC
• Low-Low (Cluster): counties that have low GDPPC surrounded by counties with low GDPPC

5.4.2 Local Moran’s I and p-values

Plot both the local Moran’s I values map and its corresponding p-values map next to each other for easier comparison.

The code chunk below will be used to create such visualisation.

gdppc <- qtm(hunan, "GDPPC") +
  tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 1.2,
            legend.text.size = 1)

hunan.localMI$quadrant <- quadrant
colors <- c("#eeeae2", "#2c7bb6", "#abd9e9", "#fdae61", "#d7191c")
clusters <- c("insignificant", "low-low", "low-high", "high-low", "high-high")

LISAmap <- tm_shape(hunan.localMI) +
  tm_fill(col = "quadrant", 
          style = "cat", 
          palette = colors[c(sort(unique(quadrant)))+1], 
          labels = clusters[c(sort(unique(quadrant)))+1],
          popup.vars = c("")) +
  tm_view(set.zoom.limits = c(11,17)) +
  tm_borders(alpha=0.5) +
  tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 1.2,
            legend.text.size = 1)

tmap_arrange(gdppc, LISAmap, 
             asp=1, ncol=2)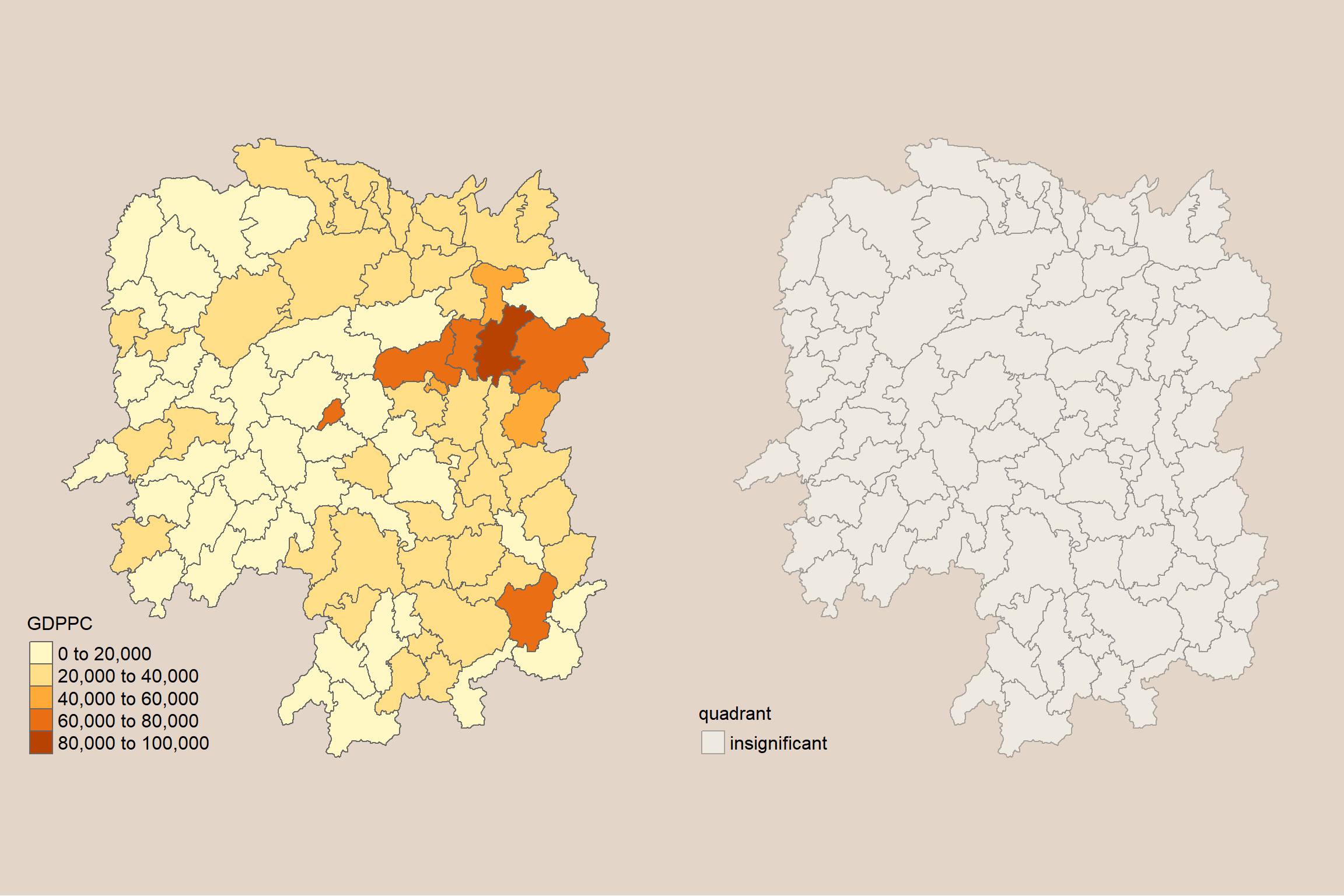

Question: What statistical observations can you draw from the LISA map above?

• We should look at the original value to make sense of the previous map.
• Focusing on the Low-High, the original map does not show any high values.
• HighHigh cluster is definitely correct.
• But the low-low cluster should be a Low-high outlier.

We can also include the local Moran’s I map and p-value map as shown below for easy comparison.

tmap_arrange(localMI.map, pvalue.map, 
             asp=1, ncol=2)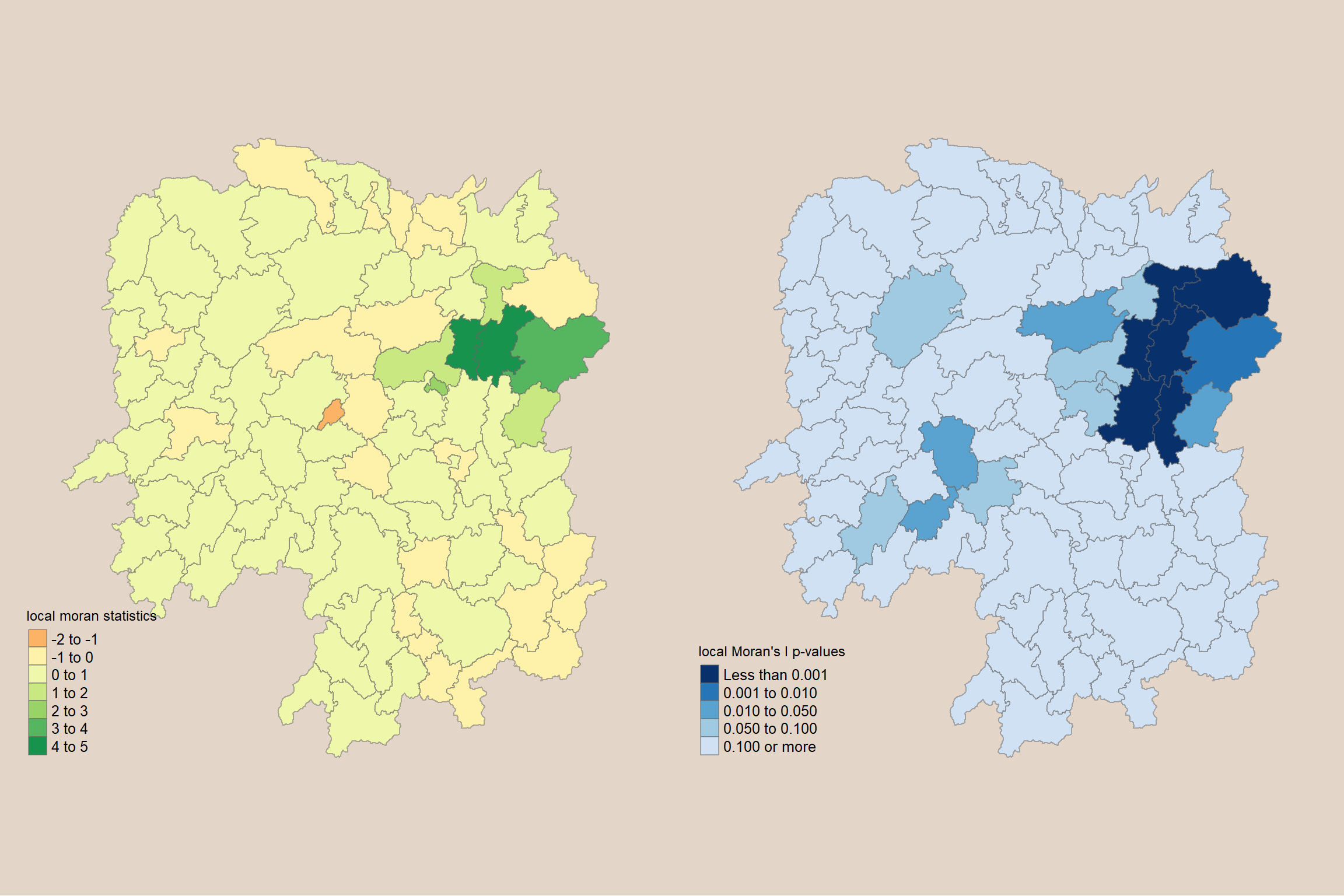

6 Hot Spot and Cold Spot Area Analysis

Besides detecting cluster and outliers, localised spatial statistics can be also used to detect hot spot and/or cold spot areas.

The term ‘hot spot’ has been used generically across disciplines to describe a region or value that is higher relative to its surroundings (Lepers et al 2005, Aben et al 2012, Isobe et al 2015).

6.1 Getis and Ord’s G-Statistics

NOTE: If you have negative values, you cannot use Getis and Ord’s G Stats. It must be all positive. Must calculated the distance based matrix and not contiguity matrix.

• Used to to detect spatial anomalies is the Getis and Ord’s G-statistics .

• Looks at neighbours within a defined proximity to identify where either high or low values clutser spatially.

• Here, statistically significant hot-spots are recognised as areas of high values where other areas within a neighbourhood range also share high values too.

The analysis consists of three steps:

1. Deriving spatial weight matrix
2. Computing Gi statistics
3. Mapping Gi statistics

6.1.1 Deriving distance-based weight matrix

First, we need to define a new set of neighbours. While the spatial autocorrelation considered units which shared borders, for Getis-Ord we are defining neighbours based on distance.

There are two type of distance-based proximity matrix, they are:

• fixed distance weight matrix; and
• adaptive distance weight matrix.

6.1.1.1 Deriving the centroid

• We will need points to associate with each polygon before we can make our connectivity graph.

• It will be a little more complicated than just running st_centroid() on the sf object: us.bound. We need the coordinates in a separate data frame for this to work.

• Use mapping function: applies a given function to each element of a vector and returns a vector of the same length. The input vector is geometry column of us.bound. The function will be st_centroid(). We will be using map_dbl variation of map from the purrr package.

• To get longitude values we map the st_centroid() function over the geometry column of us.bound and access the longitude value through double bracket notation [[]] and 1. This allows us to get only the longitude, which is the first value in each centroid.

longitude <- map_dbl(hunan$geometry, ~st_centroid(.x)[[1]])

Do the same for latitude with one key difference: We will access the second value per each centroid with [[2]].

latitude <- map_dbl(hunan$geometry, ~st_centroid(.x)[[2]])

Use cbind() to put longitude and latitude into the same object.

coords <- cbind(longitude, latitude)

6.1.1.2 Determine the cut-off distance

Firstly, we need to determine the upper limit for distance band by using the steps below:

• Return a matrix with the indices of points belonging to the set of the k nearest neighbours of each other by using knearneigh() of spdep.
• Convert the knn object returned by knearneigh() into a neighbours list of class nb with a list of integer vectors containing neighbour region number ids by using knn2nb().
• Return the length of neighbour relationship edges by using nbdists() of spdep. The function returns in the units of the coordinates if the coordinates are projected, in km otherwise.
• Remove the list structure of the returned object by using unlist().

#coords <- coordinates(hunan)
k1 <- knn2nb(knearneigh(coords))
k1dists <- unlist(nbdists(k1, coords, longlat = TRUE))
summary(k1dists)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  24.79   32.57   38.01   39.07   44.52   61.79 

Results above show that: - The largest first nearest neighbour distance is 61.79 km, so using this as the upper threshold gives certainty that all units will have at least one neighbour. - We will round up to 62 to ensure that all counties will have at least 1 nearest neighbour.

6.1.1.3 Computing fixed distance weight matrix

Compute the distance weight matrix by using dnearneigh() as shown in the code chunk below.

wm_d62 <- dnearneigh(coords, 0, 62, longlat = TRUE)
wm_d62

Neighbour list object:
Number of regions: 88 
Number of nonzero links: 324 
Percentage nonzero weights: 4.183884 
Average number of links: 3.681818 

Next, nb2listw() is used to convert the nb object into spatial weights object. The input of nb2listw() must be an object of class nb. The syntax of the function has two major arguments, namely style and zero.poly.

• style can take values “W”, “B”, “C”, “U”, “minmax” and “S”.
  • • B is the basic binary coding
  • • W is row standardised (sums over all links to n),
  • • C is globally standardised (sums over all links to n),
  • • U is equal to C divided by the number of neighbours (sums over all links to unity)
  • • S is the variance-stabilizing coding scheme proposed by Tiefelsdorf et al. 1999, p. 167-168 (sums over all links to n).

The output spatial weights object is called wm62_lw.

wm62_lw <- nb2listw(wm_d62, style = 'B')
summary(wm62_lw)

Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 324 
Percentage nonzero weights: 4.183884 
Average number of links: 3.681818 
Link number distribution:

 1  2  3  4  5  6 
 6 15 14 26 20  7 
6 least connected regions:
6 15 30 32 56 65 with 1 link
7 most connected regions:
21 28 35 45 50 52 82 with 6 links

Weights style: B 
Weights constants summary:
   n   nn  S0  S1   S2
B 88 7744 324 648 5440

6.1.1.4 Computing adaptive distance weight matrix

One of the characteristics of fixed distance weight matrix is that more densely settled areas (usually the urban areas) tend to have more neighbours and the less densely settled areas (usually the rural counties) tend to have lesser neighbours. Having many neighbours smoothes the neighbour relationship across more neighbours.

It is possible to control the numbers of neighbours directly using k-nearest neighbours, either accepting asymmetric neighbours or imposing symmetry as shown in the code chunk below.

In the example below, we fix the number of neighbours to 8.

knn <- knn2nb(knearneigh(coords, 
                         k=8)) #<<
knn

Neighbour list object:
Number of regions: 88 
Number of nonzero links: 704 
Percentage nonzero weights: 9.090909 
Average number of links: 8 
Non-symmetric neighbours list

Next, nb2listw() is used to convert the nb object into spatial weights object.

knn_lw <- nb2listw(knn, style = 'B')
summary(knn_lw)

Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 704 
Percentage nonzero weights: 9.090909 
Average number of links: 8 
Non-symmetric neighbours list
Link number distribution:

 8 
88 
88 least connected regions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 with 8 links
88 most connected regions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 with 8 links

Weights style: B 
Weights constants summary:
   n   nn  S0   S1    S2
B 88 7744 704 1300 23014

6.1.2 Computing Gi statistics

6.1.2.1 Gi statistics using fixed distance

fips <- order(hunan$County)
gi.fixed <- localG(hunan$GDPPC, wm62_lw)
gi.fixed

 [1]  0.436075843 -0.265505650 -0.073033665  0.413017033  0.273070579
 [6] -0.377510776  2.863898821  2.794350420  5.216125401  0.228236603
[11]  0.951035346 -0.536334231  0.176761556  1.195564020 -0.033020610
[16]  1.378081093 -0.585756761 -0.419680565  0.258805141  0.012056111
[21] -0.145716531 -0.027158687 -0.318615290 -0.748946051 -0.961700582
[26] -0.796851342 -1.033949773 -0.460979158 -0.885240161 -0.266671512
[31] -0.886168613 -0.855476971 -0.922143185 -1.162328599  0.735582222
[36] -0.003358489 -0.967459309 -1.259299080 -1.452256513 -1.540671121
[41] -1.395011407 -1.681505286 -1.314110709 -0.767944457 -0.192889342
[46]  2.720804542  1.809191360 -1.218469473 -0.511984469 -0.834546363
[51] -0.908179070 -1.541081516 -1.192199867 -1.075080164 -1.631075961
[56] -0.743472246  0.418842387  0.832943753 -0.710289083 -0.449718820
[61] -0.493238743 -1.083386776  0.042979051  0.008596093  0.136337469
[66]  2.203411744  2.690329952  4.453703219 -0.340842743 -0.129318589
[71]  0.737806634 -1.246912658  0.666667559  1.088613505 -0.985792573
[76]  1.233609606 -0.487196415  1.626174042 -1.060416797  0.425361422
[81] -0.837897118 -0.314565243  0.371456331  4.424392623 -0.109566928
[86]  1.364597995 -1.029658605 -0.718000620
attr(,"internals")
               Gi      E(Gi)        V(Gi)        Z(Gi) Pr(z != E(Gi))
 [1,] 0.064192949 0.05747126 2.375922e-04  0.436075843   6.627817e-01
 [2,] 0.042300020 0.04597701 1.917951e-04 -0.265505650   7.906200e-01
 [3,] 0.044961480 0.04597701 1.933486e-04 -0.073033665   9.417793e-01
 [4,] 0.039475779 0.03448276 1.461473e-04  0.413017033   6.795941e-01
 [5,] 0.049767939 0.04597701 1.927263e-04  0.273070579   7.847990e-01
 [6,] 0.008825335 0.01149425 4.998177e-05 -0.377510776   7.057941e-01
 [7,] 0.050807266 0.02298851 9.435398e-05  2.863898821   4.184617e-03
 [8,] 0.083966739 0.04597701 1.848292e-04  2.794350420   5.200409e-03
 [9,] 0.115751554 0.04597701 1.789361e-04  5.216125401   1.827045e-07
[10,] 0.049115587 0.04597701 1.891013e-04  0.228236603   8.194623e-01
[11,] 0.045819180 0.03448276 1.420884e-04  0.951035346   3.415864e-01
[12,] 0.049183846 0.05747126 2.387633e-04 -0.536334231   5.917276e-01
[13,] 0.048429181 0.04597701 1.924532e-04  0.176761556   8.596957e-01
[14,] 0.034733752 0.02298851 9.651140e-05  1.195564020   2.318667e-01
[15,] 0.011262043 0.01149425 4.945294e-05 -0.033020610   9.736582e-01
[16,] 0.065131196 0.04597701 1.931870e-04  1.378081093   1.681783e-01
[17,] 0.027587075 0.03448276 1.385862e-04 -0.585756761   5.580390e-01
[18,] 0.029409313 0.03448276 1.461397e-04 -0.419680565   6.747188e-01
[19,] 0.061466754 0.05747126 2.383385e-04  0.258805141   7.957856e-01
[20,] 0.057656917 0.05747126 2.371303e-04  0.012056111   9.903808e-01
[21,] 0.066518379 0.06896552 2.820326e-04 -0.145716531   8.841452e-01
[22,] 0.045599896 0.04597701 1.928108e-04 -0.027158687   9.783332e-01
[23,] 0.030646753 0.03448276 1.449523e-04 -0.318615290   7.500183e-01
[24,] 0.035635552 0.04597701 1.906613e-04 -0.748946051   4.538897e-01
[25,] 0.032606647 0.04597701 1.932888e-04 -0.961700582   3.362000e-01
[26,] 0.035001352 0.04597701 1.897172e-04 -0.796851342   4.255374e-01
[27,] 0.012746354 0.02298851 9.812587e-05 -1.033949773   3.011596e-01
[28,] 0.061287917 0.06896552 2.773884e-04 -0.460979158   6.448136e-01
[29,] 0.014277403 0.02298851 9.683314e-05 -0.885240161   3.760271e-01
[30,] 0.009622875 0.01149425 4.924586e-05 -0.266671512   7.897221e-01
[31,] 0.014258398 0.02298851 9.705244e-05 -0.886168613   3.755267e-01
[32,] 0.005453443 0.01149425 4.986245e-05 -0.855476971   3.922871e-01
[33,] 0.043283712 0.05747126 2.367109e-04 -0.922143185   3.564539e-01
[34,] 0.020763514 0.03448276 1.393165e-04 -1.162328599   2.451020e-01
[35,] 0.081261843 0.06896552 2.794398e-04  0.735582222   4.619850e-01
[36,] 0.057419907 0.05747126 2.338437e-04 -0.003358489   9.973203e-01
[37,] 0.013497133 0.02298851 9.624821e-05 -0.967459309   3.333145e-01
[38,] 0.019289310 0.03448276 1.455643e-04 -1.259299080   2.079223e-01
[39,] 0.025996272 0.04597701 1.892938e-04 -1.452256513   1.464303e-01
[40,] 0.016092694 0.03448276 1.424776e-04 -1.540671121   1.233968e-01
[41,] 0.035952614 0.05747126 2.379439e-04 -1.395011407   1.630124e-01
[42,] 0.031690963 0.05747126 2.350604e-04 -1.681505286   9.266481e-02
[43,] 0.018750079 0.03448276 1.433314e-04 -1.314110709   1.888090e-01
[44,] 0.015449080 0.02298851 9.638666e-05 -0.767944457   4.425202e-01
[45,] 0.065760689 0.06896552 2.760533e-04 -0.192889342   8.470456e-01
[46,] 0.098966900 0.05747126 2.326002e-04  2.720804542   6.512325e-03
[47,] 0.085415780 0.05747126 2.385746e-04  1.809191360   7.042128e-02
[48,] 0.038816536 0.05747126 2.343951e-04 -1.218469473   2.230456e-01
[49,] 0.038931873 0.04597701 1.893501e-04 -0.511984469   6.086619e-01
[50,] 0.055098610 0.06896552 2.760948e-04 -0.834546363   4.039732e-01
[51,] 0.033405005 0.04597701 1.916312e-04 -0.908179070   3.637836e-01
[52,] 0.043040784 0.06896552 2.829941e-04 -1.541081516   1.232969e-01
[53,] 0.011297699 0.02298851 9.615920e-05 -1.192199867   2.331829e-01
[54,] 0.040968457 0.05747126 2.356318e-04 -1.075080164   2.823388e-01
[55,] 0.023629663 0.04597701 1.877170e-04 -1.631075961   1.028743e-01
[56,] 0.006281129 0.01149425 4.916619e-05 -0.743472246   4.571958e-01
[57,] 0.063918654 0.05747126 2.369553e-04  0.418842387   6.753313e-01
[58,] 0.070325003 0.05747126 2.381374e-04  0.832943753   4.048765e-01
[59,] 0.025947288 0.03448276 1.444058e-04 -0.710289083   4.775249e-01
[60,] 0.039752578 0.04597701 1.915656e-04 -0.449718820   6.529132e-01
[61,] 0.049934283 0.05747126 2.334965e-04 -0.493238743   6.218439e-01
[62,] 0.030964195 0.04597701 1.920248e-04 -1.083386776   2.786368e-01
[63,] 0.058129184 0.05747126 2.343319e-04  0.042979051   9.657182e-01
[64,] 0.046096514 0.04597701 1.932637e-04  0.008596093   9.931414e-01
[65,] 0.012459080 0.01149425 5.008051e-05  0.136337469   8.915545e-01
[66,] 0.091447733 0.05747126 2.377744e-04  2.203411744   2.756574e-02
[67,] 0.049575872 0.02298851 9.766513e-05  2.690329952   7.138140e-03
[68,] 0.107907212 0.04597701 1.933581e-04  4.453703219   8.440175e-06
[69,] 0.019616151 0.02298851 9.789454e-05 -0.340842743   7.332220e-01
[70,] 0.032923393 0.03448276 1.454032e-04 -0.129318589   8.971056e-01
[71,] 0.030317663 0.02298851 9.867859e-05  0.737806634   4.606320e-01
[72,] 0.019437582 0.03448276 1.455870e-04 -1.246912658   2.124295e-01
[73,] 0.055245460 0.04597701 1.932838e-04  0.666667559   5.049845e-01
[74,] 0.074278054 0.05747126 2.383538e-04  1.088613505   2.763244e-01
[75,] 0.013269580 0.02298851 9.719982e-05 -0.985792573   3.242349e-01
[76,] 0.049407829 0.03448276 1.463785e-04  1.233609606   2.173484e-01
[77,] 0.028605749 0.03448276 1.455139e-04 -0.487196415   6.261191e-01
[78,] 0.039087662 0.02298851 9.801040e-05  1.626174042   1.039126e-01
[79,] 0.031447120 0.04597701 1.877464e-04 -1.060416797   2.889550e-01
[80,] 0.064005294 0.05747126 2.359641e-04  0.425361422   6.705732e-01
[81,] 0.044606529 0.05747126 2.357330e-04 -0.837897118   4.020885e-01
[82,] 0.063700493 0.06896552 2.801427e-04 -0.314565243   7.530918e-01
[83,] 0.051142205 0.04597701 1.933560e-04  0.371456331   7.102977e-01
[84,] 0.102121112 0.04597701 1.610278e-04  4.424392623   9.671399e-06
[85,] 0.021901462 0.02298851 9.843172e-05 -0.109566928   9.127528e-01
[86,] 0.064931813 0.04597701 1.929430e-04  1.364597995   1.723794e-01
[87,] 0.031747344 0.04597701 1.909867e-04 -1.029658605   3.031703e-01
[88,] 0.015893319 0.02298851 9.765131e-05 -0.718000620   4.727569e-01
attr(,"cluster")
 [1] Low  Low  High High High High High High High Low  Low  High Low  Low  Low 
[16] High High High High Low  High High Low  Low  High Low  Low  Low  Low  Low 
[31] Low  Low  Low  High Low  Low  Low  Low  Low  Low  High Low  Low  Low  Low 
[46] High High Low  Low  Low  Low  High Low  Low  Low  Low  Low  High Low  Low 
[61] Low  Low  Low  High High High Low  High Low  Low  High Low  High High Low 
[76] High Low  Low  Low  Low  Low  Low  High High Low  High Low  Low 
Levels: Low High
attr(,"gstari")
[1] FALSE
attr(,"call")
localG(x = hunan$GDPPC, listw = wm62_lw)
attr(,"class")
[1] "localG"

Results above show that:

• The output of localG() is a vector of G or Gstar values, with attributes “gstari” set to TRUE or FALSE, “call” set to the function call, and class “localG”.

• The Gi statistics is represented as a Z-score. Greater values represent a greater intensity of clustering and the direction (positive or negative) indicates high or low clusters.

• Join the Gi values to their corresponding hunan sf data frame by using the code chunk below.

• The 3 sub tasks are:

  • Convert the output vector (i.e. gi.fixed) into r matrix object by using as.matrix().c
  • cbind() is used to join hunan data and gi.fixed matrix to produce a new SpatialPolygonDataFrame called hunan.gi. Field name of the gi values is renamed to gstat_fixed by using names().

hunan.gi <- cbind(hunan, as.matrix(gi.fixed)) %>%
  rename(gstat_fixed = as.matrix.gi.fixed.)

hunan.gi

Simple feature collection with 88 features and 9 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84
First 10 features:
     NAME_2  ID_3    NAME_3   ENGTYPE_3    County GDPPC      Z.GDPPC lag_GDPPC
1   Changde 21098   Anxiang      County   Anxiang 23667 -0.049205949  24847.20
2   Changde 21100   Hanshou      County   Hanshou 20981 -0.228341158  22724.80
3   Changde 21101    Jinshi County City    Jinshi 34592  0.679406172  24143.25
4   Changde 21102        Li      County        Li 24473  0.004547952  27737.50
5   Changde 21103     Linli      County     Linli 25554  0.076642204  27270.25
6   Changde 21104    Shimen      County    Shimen 27137  0.182215933  21248.80
7  Changsha 21109   Liuyang County City   Liuyang 63118  2.581867439  43747.00
8  Changsha 21110 Ningxiang      County Ningxiang 62202  2.520777398  33582.71
9  Changsha 21111 Wangcheng      County Wangcheng 70666  3.085260051  45651.17
10 Chenzhou 21112     Anren      County     Anren 12761 -0.776550918  32027.62
   gstat_fixed                       geometry
1   0.43607584 POLYGON ((112.0625 29.75523...
2  -0.26550565 POLYGON ((112.2288 29.11684...
3  -0.07303367 POLYGON ((111.8927 29.6013,...
4   0.41301703 POLYGON ((111.3731 29.94649...
5   0.27307058 POLYGON ((111.6324 29.76288...
6  -0.37751078 POLYGON ((110.8825 30.11675...
7   2.86389882 POLYGON ((113.9905 28.5682,...
8   2.79435042 POLYGON ((112.7181 28.38299...
9   5.21612540 POLYGON ((112.7914 28.52688...
10  0.22823660 POLYGON ((113.1757 26.82734...

6.1.2.2 Mapping Gi values with fixed distance weights

The code chunk below shows the functions used to map the Gi values derived using fixed distance weight matrix.

gdppc <- qtm(hunan, "GDPPC") +
    tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 1.2,
            legend.text.size = 1)

Gimap <-tm_shape(hunan.gi) +
  tm_fill(col = "gstat_fixed", 
          style = "pretty",
          palette="-RdBu",
          title = "local Gi") +
  tm_borders(alpha = 0.5) +
    tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 1.2,
            legend.text.size = 1)

tmap_arrange(gdppc, Gimap, asp=1, ncol=2)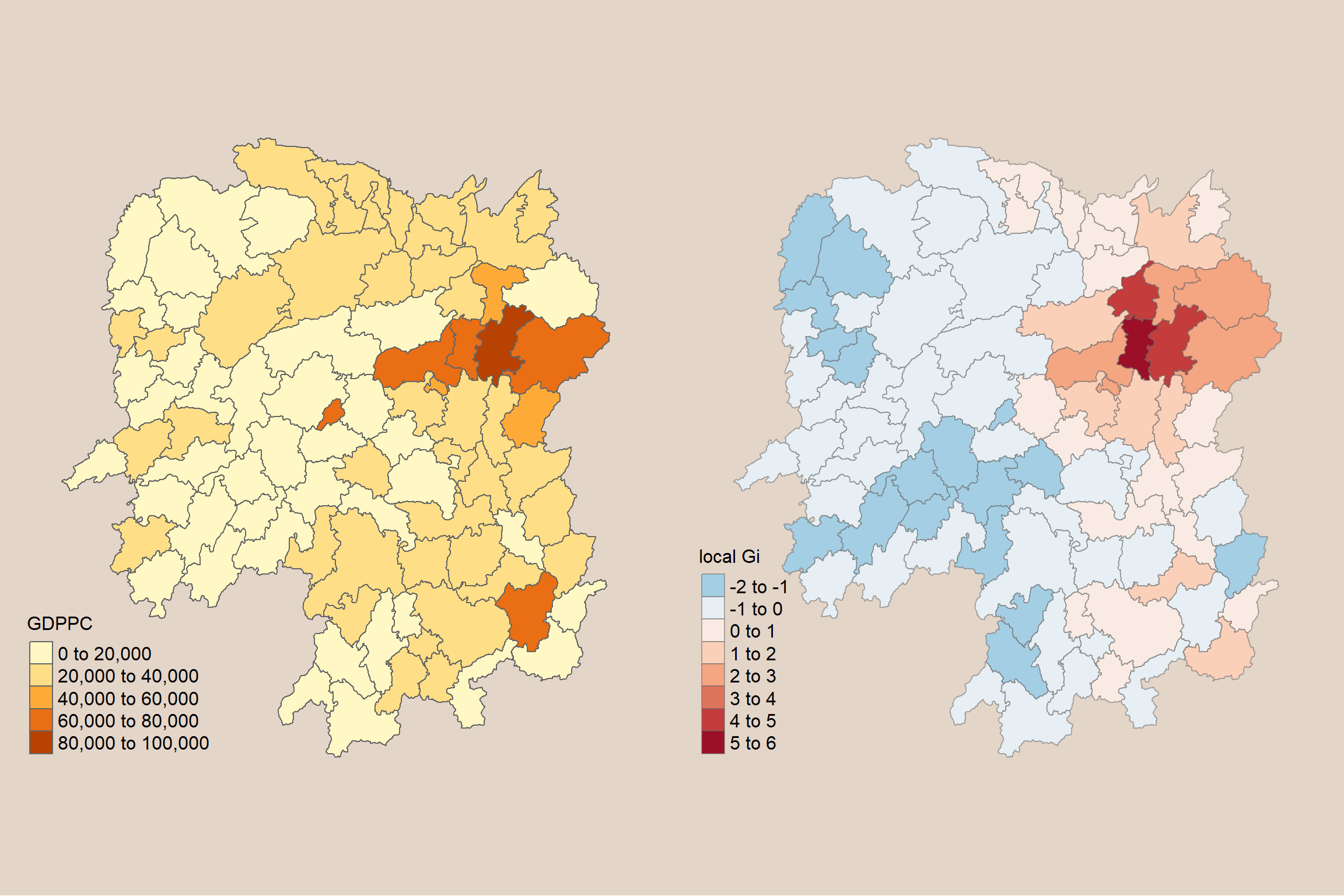

Question: What statistical observation can you draw from the Gi map above?

• In the left side, western region is the cold spot area while the hot spot area is in the east side.
• If you plot the transportation line, you can see that it is mainly on the east side. So this might be one of the underlying reason why the hot spot areas are on the right side.

6.1.2.3 Gi statistics using adaptive distance

The code chunk below are used to compute the Gi values for GDPPC2012 by using an adaptive distance weight matrix (i.e knb_lw).

fips <- order(hunan$County)
gi.adaptive <- localG(hunan$GDPPC, knn_lw)
hunan.gi <- cbind(hunan, as.matrix(gi.adaptive)) %>%
  rename(gstat_adaptive = as.matrix.gi.adaptive.)

6.1.2.4 Mapping Gi values with adaptive distance weights

We can also visualise the locations of hot spot and cold spot areas.

The code chunk below shows the functions used to map the Gi values derived using fixed distance weight matrix.

gdppc<- qtm(hunan, "GDPPC")+
      tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 1.2,
            legend.text.size = 1)

Gimap2 <- tm_shape(hunan.gi) +
  tm_fill(col = "gstat_adaptive", 
          style = "pretty",
          palette="-RdBu",
          title = "local Gi") +
  tm_borders(alpha = 0.5) +
  tm_layout(bg.color = "#E4D5C9",
            frame = F,
            legend.title.size = 1.2,
            legend.text.size = 1)

tmap_arrange(gdppc, 
             Gimap2, 
             asp=1, 
             ncol=2)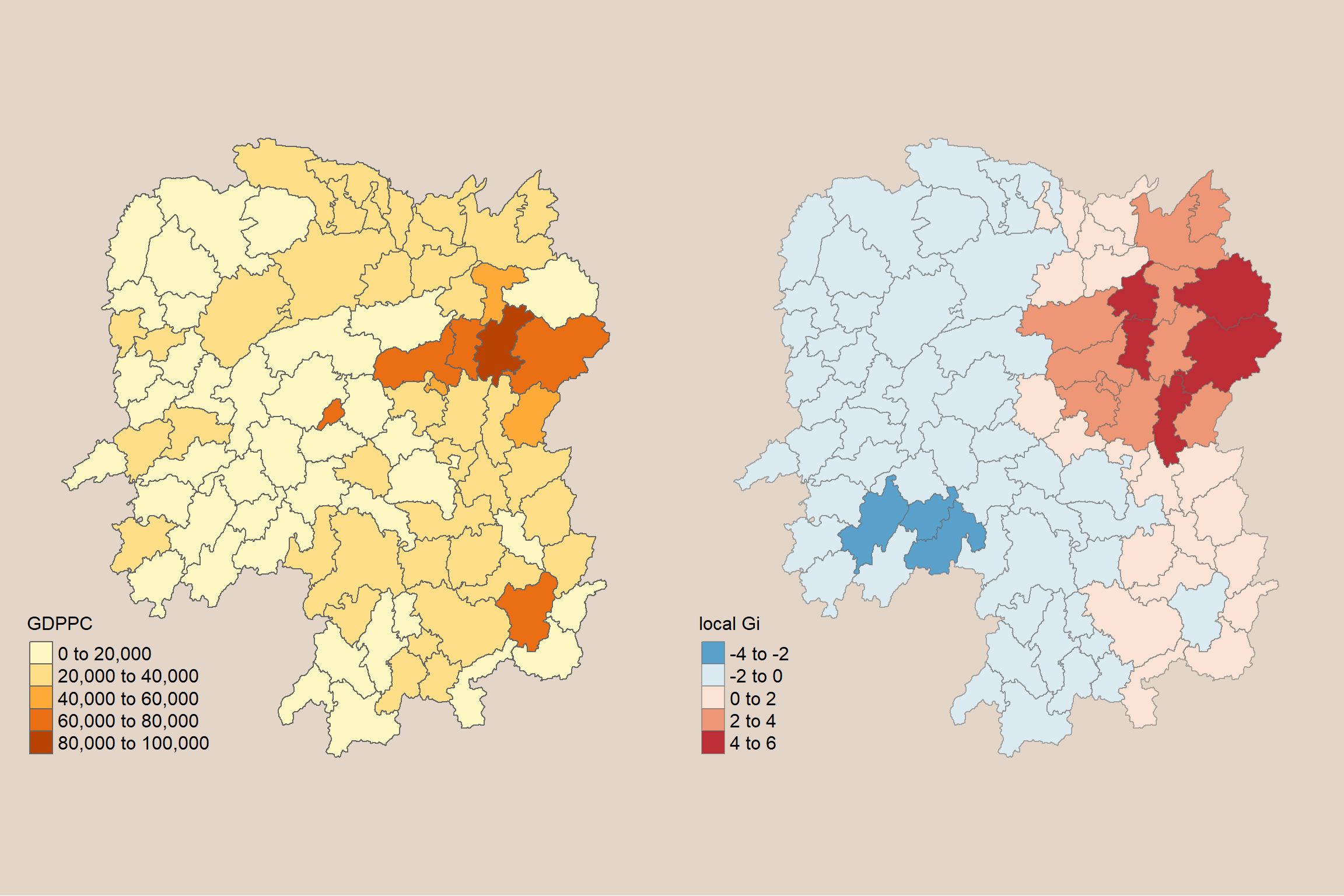

Question: What statistical observation can you draw from the Gi map above?

• This plot with the adaptive weights is actually smoother than the previous map with fixed weights
• The range in the legend has also changed

6 Reference

Kam, T. S. Lobal Measures of Spatial Autocorrelation. R for Geospatial Data Science and Analytics. https://r4gdsa.netlify.app/chap10.html